主方法

2025年3月17日 | 阅读 3 分钟

主方法用于解决以下类型的递归式

T (n) = a T DAA Master Method + f (n) 其中 a≥1 且 b≥1 是常数，f(n) 是一个函数，可以解释为

设 T (n) 在非负整数上定义，由递归式得到。

 T (n) = a T+ f (n)

在递归算法的函数分析中，常量和函数具有以下意义

n 是问题的规模。
a 是递归中子问题的数量。
n/b 是每个子问题的规模。（这里假设所有子问题的规模基本相同。）
f (n) 是在递归调用之外完成的工作的总和，包括划分问题和组合子问题解的总和。
不可能总是根据要求限制函数，所以我们设置了三种情况，告诉我们可以在函数上应用什么样的界限。

主定理

可以在这三种情况下完成渐近紧界

情况 1：如果 f (n) = DAA Master Method 对于某个常数 ε >0，则得出

T (n) = Θ

示例

T (n) = 8 T  apply master theorem on it.

解决方案

Compare T (n) = 8 T  with 
 T (n) = a T 
 a = 8, b=2, f (n) = 1000 n², log_ba = log₂8 = 3
 Put all the values in: f (n) = 
     1000 n² = O (n^3-ε ) 
     If we choose ε=1, we get: 1000 n² = O (n^3-1) = O (n²)

由于该等式成立，主定理的第一种情况适用于给定的递归关系，从而得出结论

T (n) = Θ 
   Therefore: T (n) = Θ (n³)

情况 2：如果对于某个常数 k ≥ 0，以下成立

F (n) = Θ  then it follows that: T (n) = Θ

示例

T (n) = 2 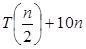, solve the recurrence by using the master method.
As compare the given problem with T (n) = a T a = 2, b=2, k=0, f (n) = 10n, log_ba = log₂2 =1 
Put all the values in f (n) =Θ , we will get 
	10n = Θ (n¹) = Θ (n) which is true.
Therefore: T (n) = Θ 
      = Θ (n log n)

情况 3：如果 f(n) = Ω DAA Master Method 对于某个常数 ε >0，并且也成立：a f 对于某个常数 c<1 对于较大的 n 值，则

示例： 解决递归关系

T (n) = 2

解决方案

Compare the given problem with T (n) = a T 
a= 2, b =2, f (n) = n², log_ba = log₂2 =1 
Put all the values in f (n) = Ω  ..... (Eq. 1)
If we insert all the value in (Eq.1), we will get 
  n² = Ω(n^1+ε) put ε =1, then the equality will hold.
  n² = Ω(n¹⁺¹) = Ω(n²)
Now we will also check the second condition:
  2 
If we will choose c =1/2, it is true:
    ∀ n ≥1 
So it follows: T (n) = Θ ((f (n))
    T (n) = Θ(n²)