最优子结构属性

如果一个给定问题的最优解可以通过找到所有子问题的最优解来获得，那么该问题就具有最优子结构属性。换句话说，我们可以通过解决较小的问题来解决较大的问题。假设我们有一个复杂的问题，那么我们将把这个问题最优地分解成更简单的问题，以找到给定复杂问题的最优解。

例如：f(n) = f(n-1) + f(n-2)

在上面的例子中，问题 f(n) 被分解为两个较小的问题，即 F(n-1) 和 f(n-2)。这两个较小的问题可以进一步分解为更小的问题。

上图显示了问题如何分解为子问题。这个过程将一直持续到问题无法进一步分解。一旦子问题不能进一步分解，我们将采用基本情况来找到解决方案。

最优性原理

Richard Bellman 是一位在 1957 年研究动态规划的科学家。

让我们通过一个例子来理解最优性。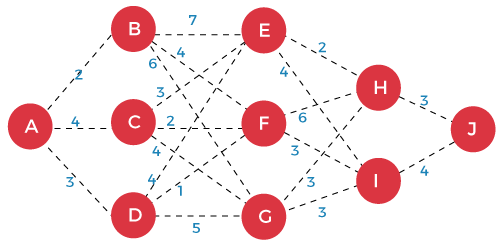

设 F(x) 是从节点 X 到 J 所需的最小距离。假设 F(J) = 0。从顶点 H 到顶点 J 的距离是 3，从顶点 I 到顶点 J 的距离是 4。

现在我们计算从顶点 E 到顶点 J 的距离，如下所示

F(E) = min{ 1+F(H), 4+F(I)}

=min{4, 8}

最小值为 4；因此，从顶点 E 到顶点 J 的距离将为 4。

现在我们计算从顶点 F 到顶点 J 的距离，如下所示

F(F) = min{ 6+F(H), 3+F(I)}

= min{9, 7}

最小值为 7；因此，从顶点 F 到顶点 J 的距离将为 7。

现在我们计算从顶点 G 到顶点 J 的距离，如下所示

F(G) = min{ 3+F(H), 3+F(I)}

= min{6, 7}

最小值为 6；因此，从顶点 G 到顶点 J 的距离将为 6。

现在我们计算从顶点 B 到顶点 J 的距离，如下所示

F(B) = min{ 7+F(E), 4+F(F), 6+F(G)}

= min{11, 11, 12}

最小值为 11；因此，从顶点 B 到顶点 J 的距离将为 11。

现在我们计算从顶点 C 到顶点 J 的距离，如下所示

F(C) = min{ 3+F(E), 2+F(F), 4+F(G)}

= min{6, 4, 8}

最小值为 4；因此，从顶点 C 到顶点 J 的距离将为 11。

现在我们计算从顶点 D 到顶点 J 的距离，如下所示

F(D) = min{ 4+F(E), 1+F(F), 5+F(G)}

= min{8, 8, 11}

最小值为 8；因此，从顶点 D 到顶点 J 的距离将为 8。

现在我们计算从顶点 A 到顶点 J 的距离，如下所示

F(A) = min{ 2+F(B), 4+F(C), 3+F(D)}

= min{13, 11, 11}

最小值为 11；因此，从顶点 A 到顶点 J 的距离将为 11。所以，我们可以说从 A 到 J 的最小距离是 11。现在，我们有两种方式通过顶点 D 从顶点 A 到 J

• 第一种方式是从顶点 A 到顶点 D，然后 D 到 F，F 到 I，然后 I 到 J。
• 第二种方式是从顶点 A 到顶点 D，然后 D 到 E，然后 E 到 H，然后 H 到 J。

在这里，我们通过子问题构建了一个最优解。因此，我们可以说上述问题具有最优子结构。

我们可以通过反证法证明上述问题。

设 R_a..._j 是从节点 A 到 J 的最优路径。

我们假设这条最优路径通过节点 k 到达目的地。

现在，路径可以分为 R_a.._k 和 R_k..._J

让我们通过图示来理解。

假设存在一条从 A 到 K 的较短路径，并将其命名为 R`_a.._k

如果 R`_a.._k < R_a.._k

那么 R`_a.._k + R_k.._j < R_a.._k + R_k.._j

上述关系不可能成立，因为我们已经知道 R_a.._k + R_k.._j 是一个最优解，如前所述。因此，R`_a.._k，一个从 A 到 K 的较短路径不存在，并且 R_a.._k + R_k.._j 确实是最优解。

没有最优子结构的问题

两个问题可能没有最优子结构

• 最长路径问题
• 最大团问题

我们首先来看看最长路径问题。

考虑下面有 5 个顶点的图。

问题的目标是在不重复边的情况下找到两个顶点之间的最长路径。假设我们要找到从 A 到 C 的最长路径，即 LongestPath(A, C)。有两条路可以从 A 到 C

• 首先，我们从 A 到 E，E 到 D，然后 D 到 C。
• 第二种方式是从 A 到 B，然后 B 到 C。

第一种方式提供了最长路径的解决方案，因为第二种方式没有提供最长路径。最优性原理如下所示

上图描绘了从 A 到 B，然后 B 到 C 的路径，这是最优解。但最优路径不是最长路径的解决方案。

如果最优性原理适用于最长路径问题，那么我们应该将问题分解成子部分。从 A 到 C 的最长路径可以写成

Longestpath(A, C) = Longest_path(A, D) + (D-C)

有两种可能的方法可以找到从 A 到 D 的最长路径

• 第一种方式是从 A 到 E，然后 E 到 D。
• 第二种方式是从 A 到 B，B 到 C，然后 C 到 D。

第二种方式提供了最长路径。如果我们将此路径添加到边 (D-C)，将会出现重复的边，即 D 到 C，这是不允许的。因此，在这种情况下，问题的子解不能组合形成整体最优解。因此，我们可以说最长路径问题不具有最优子结构。

最大团问题

在这里，团意味着所有顶点彼此相连。最大团意味着图中顶点最多的团。让我们通过一个例子来理解最大团。

考虑下面的图

顶点：{1, 2, 3, 4, 5, 6, 7, 8, 9}

最大团：{5, 6, 7, 8, 9}

如果最优性原理适用于最大团问题，那么我们应该将问题分解为子部分

顶点 = {1, 2, 3, 4, 5, 6, 7} + {8, 9}

最大团 = {5, 6, 7, 8, 9}

团 = {1, 2, 3, 4}, {5, 6, 7} + {8, 9}