动态规划

动态规划是一种技术，它将问题分解为子问题，并保存结果以备将来使用，这样我们就无需重复计算结果。优化子问题以优化整体解决方案称为最优子结构属性。动态规划的主要用途是解决优化问题。这里的优化问题是指我们试图找出问题的最小值或最大值。如果存在解决方案，动态规划保证能找到问题的最优解决方案。

动态规划的定义是，它是一种通过首先将复杂问题分解为一系列更简单的子问题，只计算每个子问题一次，然后存储它们的解决方案以避免重复计算来解决复杂问题的一种技术。

让我们通过一个例子来理解这种方法。

考虑斐波那契数列的例子。下面的数列是斐波那契数列

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ,…

上述数列中的数字不是随机计算的。从数学上讲，我们可以使用下面的公式来写出每个项

F(n) = F(n-1) + F(n-2)，

基本值为 F(0) = 0，F(1) = 1。为了计算其他数字，我们遵循上述关系。例如，F(2) 是 **f(0)** 和 **f(1)** 的和，等于 1。

如何计算 F(20)？

F(20) 项将使用斐波那契数列的第 n 个公式进行计算。下图显示了 F(20) 的计算过程。

正如我们在上图中观察到的，F(20) 是通过 F(19) 和 F(18) 的和计算的。在动态规划方法中，我们尝试将问题分解为相似的子问题。在上述情况下，我们将 F(20) 分解为相似的子问题，即 F(19) 和 F(18)。如果我们回顾动态规划的定义，它说相似的子问题不应计算超过一次。然而，在上述情况下，子问题被计算了两次。在上面的例子中，F(18) 被计算了两次；类似地，F(17) 也被计算了两次。然而，这项技术非常有用，因为它解决了相似的子问题，但我们需要小心存储结果，因为我们不特别注意存储已计算一次的结果，这可能会导致资源浪费。

在上面的例子中，如果我们计算右子树中的 F(18)，那么它将导致大量的资源使用并降低整体性能。

上述问题的解决方案是将计算结果保存在数组中。首先，我们计算 F(16) 和 F(17) 并将它们的值保存在数组中。F(18) 通过对数组中已保存的 F(17) 和 F(16) 的值求和来计算。计算出的 F(18) 值保存在数组中。F(19) 的值是通过 F(18) 和 F(17) 的和计算的，它们的值已保存在数组中。计算出的 F(19) 值存储在数组中。F(20) 的值可以通过将 F(19) 和 F(18) 的值相加来计算，并且 F(19) 和 F(18) 的值都已保存在数组中。计算出的 F(20) 的最终值存储在数组中。

动态规划方法是如何工作的？

以下是动态规划遵循的步骤

• 它将复杂问题分解为更简单的子问题。
• 它找到这些子问题的最优解。
• 它存储子问题的结果（记忆化）。存储子问题结果的过程称为记忆化。
• 它重用它们，以便同一个子问题不会计算多次。
• 最后，计算复杂问题的结果。

以上五个步骤是动态规划的基本步骤。动态规划适用于具有以下性质的问题

那些具有重叠子问题和最优子结构的问题。这里的最优子结构意味着优化问题的解决方案可以通过简单地组合所有子问题的最优解决方案来获得。

在动态规划的情况下，空间复杂度会增加，因为我们存储了中间结果，但时间复杂度会降低。

动态规划的方法

动态规划有两种方法

• 自顶向下方法
• 自底向上方法

自顶向下方法

自顶向下方法遵循记忆化技术，而自底向上方法遵循制表技术。这里的记忆化等于递归和缓存的总和。递归是指函数调用自身，而缓存是指存储中间结果。

优点

• 它非常容易理解和实现。
• 它仅在需要时才计算子问题。
• 它易于调试。

缺点

它使用占用调用栈更多内存的递归技术。有时当递归过深时，会发生堆栈溢出情况。

它占用了更多内存，从而降低了整体性能。

让我们通过一个例子来理解动态规划。

在上面的代码中，我们使用了递归方法来找出斐波那契数列。当 'n' 值增加时，函数调用也会增加，计算也会增加。在这种情况下，时间复杂度呈指数级增长，变为 2ⁿ。

解决此问题的一种方法是使用动态规划方法。与其一次又一次地生成递归树，不如重用先前计算的值。如果我们使用动态规划方法，则时间复杂度将为 O(n)。

当我们将动态规划方法应用于斐波那契数列的实现时，代码将如下所示

在上面的代码中，我们使用了记忆化技术，在该技术中，我们将结果存储在数组中以重用值。这也被称为自顶向下方法，在该方法中，我们从顶部开始将问题分解为子问题。

自底向上方法

自底向上方法也是一种可以用来实现动态规划的技术。它使用制表技术来实现动态规划方法。它解决了相同类型的问题，但消除了递归。如果我们消除了递归，就不会出现堆栈溢出问题，也不会有递归函数的开销。在这种制表技术中，我们解决问题并将结果存储在矩阵中。

有两种应用动态规划的方法

• 自顶向下
• 自底向上

自底向上方法用于避免递归，从而节省内存空间。自底向上是一种从头开始的算法，而递归算法从末尾开始并向后工作。在自底向上方法中，我们从基本情况开始找到最终答案。我们知道，斐波那契数列的基本情况是 0 和 1。由于自底向上方法从基本情况开始，所以我们将从 0 和 1 开始。

要点

• 我们解决所有较小的子问题，这些子问题将用于解决较大的子问题，然后使用较小的子问题来解决较大的问题。
• 我们使用 for 循环来迭代子问题。
• 自底向上方法也称为制表或填表法。

让我们通过一个例子来理解。

假设我们有一个数组，其 a[0] 和 a[1] 位置的值分别为 0 和 1，如下所示

由于自底向上方法从较低的值开始，因此将 a[0] 和 a[1] 的值相加以找到 a[2] 的值，如下所示

a[3] 的值将通过将 a[1] 和 a[2] 相加来计算，结果为 2，如下所示

a[4] 的值将通过将 a[2] 和 a[3] 相加来计算，结果为 3，如下所示

a[5] 的值将通过将 a[4] 和 a[3] 的值相加来计算，结果为 5，如下所示

下面提供了使用自底向上方法实现斐波那契数列的代码

在上面的代码中，基本情况是 0 和 1，然后我们使用 for 循环来查找斐波那契数列的其他值。

让我们通过图示表示来理解。

最初，前两个值，即 0 和 1，可以表示为

当 i=2 时，将 0 和 1 相加，如下所示

当 i=3 时，将 1 和 1 相加，如下所示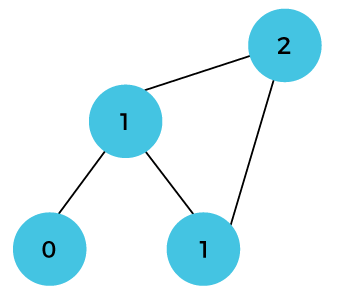

当 i=4 时，将 2 和 1 相加，如下所示

当 i=5 时，将 3 和 2 相加，如下所示

在上述情况下，我们从底部开始，到达顶部。