选择排序

选择排序通过对每次遍历只进行一次交换来改进冒泡排序。为了做到这一点，选择排序在遍历过程中寻找最大值，并在遍历结束后将其放置在最佳位置。与冒泡排序类似，第一次遍历后，最大项位于正确的位置。第二次遍历后，下一个最大项就被设置好了。这个过程持续进行，需要 n-1 次遍历才能对 n 个项目进行排序，因为最后一个项目必须在 (n-1) 次遍历后设置好。

算法：选择排序 (A)

选择排序的工作原理

1. 在选择排序中，首先，我们将初始元素设置为最小值。
2. 现在我们将最小值与第二个元素进行比较。如果第二个元素小于最小值，我们将交换它们，然后将第三个元素赋值给最小值。
3. 否则，如果第二个元素大于最小值，也就是我们的第一个元素，那么我们将什么都不做，然后移动到第三个元素，然后将其与最小值进行比较。
   我们将重复此过程，直到到达最后一个元素。
4. 在每次迭代完成后，我们会注意到我们的最小值已经到达了未排序列表的开头。
5. 对于每次迭代，我们将从未排序列表的第一个元素开始索引。我们将重复步骤 1 到 4，直到列表被排序或所有元素都被正确放置。
   考虑以下我们将使用选择排序算法排序的未排序数组示例。
   A [] = (7, 4, 3, 6, 5)。
   A [] =

1^st 迭代

设置最小值 = 7

• 比较 a₀ 和 a₁

因为，a₀ > a₁，设置最小值 = 4。

• 比较 a₁ 和 a₂

因为，a₁ > a₂，设置最小值 = 3。

• 比较 a₂ 和 a₃

因为，a₂ < a₃，设置最小值= 3。

• 比较 a₂ 和 a₄

因为，a₂ < a₄，设置最小值 =3。

由于 3 是最小元素，因此我们将交换 a₀ 和 a₂。

2^nd 迭代

设置最小值 = 4

• 比较 a₁ 和 a₂

因为，a₁ < a₂，设置最小值 = 4。

• 比较 a₁ 和 a₃

因为，A[1] < A[3]，设置最小值 = 4。

• 比较 a₁ 和 a₄

同样，a₁ < a₄，设置最小值 = 4。

由于最小值已经放置在正确的位置，因此不会进行交换。

3^rd 迭代

设置最小值 = 7

• 比较 a₂ 和 a₃

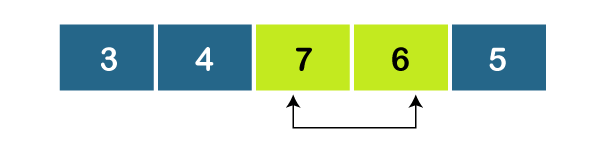因为，a₂ > a₃，设置最小值 = 6。

• 比较 a₃ 和 a₄

因为，a₃ > a₄，设置最小值 = 5。

由于 5 是剩余未排序元素中最小的元素，因此我们将交换 7 和 5。

4^th 迭代

设置最小值 = 6

• 比较 a₃ 和 a₄

因为 a₃ < a₄，设置最小值 = 6。

由于最小值已经放置在正确的位置，因此不会进行交换。

选择排序的复杂度分析

输入： 给定 n 个输入元素。

输出： 对列表进行排序所需的步骤数。

逻辑： 如果我们得到 n 个元素，那么在第一遍中，它将进行 n-1 次比较；在第二遍中，它将进行 n-2 次比较；在第三遍中，它将进行 n-3 次比较，依此类推。因此，可以通过以下方式找到比较的总数；

因此，选择排序算法包含 O(n²) 的时间复杂度和 O(1) 的空间复杂度，因为它需要一些额外的内存空间来交换 temp 变量。

时间复杂度

• 最佳情况复杂度： 选择排序算法的最佳情况时间复杂度为 O(n²)，对于已排序的数组。
• 平均情况复杂度： 选择排序算法的平均情况时间复杂度为 O(n²)，其中现有元素以混乱的顺序排列，即既不是升序也不是降序。
• 最坏情况复杂度： 最坏情况时间复杂度也是 O(n²)，当我们对数组的降序进行升序排序时会发生这种情况。

在选择排序算法中，时间复杂度在所有三种情况下都为 O(n²)。这是因为在每个步骤中，我们都需要找到 最小值 元素，以便将其放置在正确的位置。一旦我们追踪了整个数组，我们就会得到我们的最小元素。