基本执行时间模型

该模型由 J.D. Musa 于 1979 年建立，它基于执行时间。基本执行模型是最流行的、使用最广泛的可靠性增长模型，主要是因为

• 它实用、简单且易于理解。
• 它的参数与物理世界有清晰的联系。
• 它可以用于准确的可靠性预测。

基本执行模型最初使用执行时间来确定故障行为。执行时间稍后可以转换为日历时间。

故障行为是一个非齐次泊松过程，这意味着相关的概率分布是一个泊松

过程，其特征随时间变化。

它等效于具有不同均值函数的 M-O 对数泊松执行时间模型。

在这种情况下，均值函数基于指数分布。

基本执行模型中涉及的变量

故障强度 (λ): 单位时间内发生的故障数。

执行时间 (τ): 程序运行的时间。

平均经历的故障 (μ): 在一个时间间隔内平均经历的故障数。

在基本执行模型中，平均经历的故障数 μ 用执行时间 (τ) 表示为

其中

-λ₀: 代表执行开始时的初始故障强度。

-v₀: 代表无限时间内发生的总故障数；它对应于最终要观察到的预期故障数。

故障强度表示为执行时间的函数，由下式给出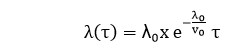

它基于以上公式。故障强度 λ 表示为 μ 的函数，如下所示

其中

λ₀: 初始

v₀: 如果程序执行无限长时间，则经历的故障数。

μ: 在给定时间段内经历的平均或预期故障数。

τ: 执行时间。

为了推导这种关系，可以将等式 1 写成

可以求解上述等式得到 λ(τ)，结果为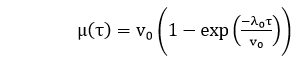

故障强度作为执行时间的函数如图所示

基于上述表达式，给定一些故障强度目标，可以计算出达到该目标所需的预期故障数 ∆λ 和额外执行时间 ∆τ。

其中

λ₀: 初始故障强度

λ_P: 当前故障强度

λ_F: 故障强度目标

∆μ: 要达到故障强度目标所需的预期额外故障数。

这可以用数学形式推导出来

示例: 假设一个程序在无限时间内将经历 200 个故障。现在已经经历了 100 个。初始故障强度为 20/hr。确定当前的故障强度。

1. 求出每个故障的故障强度递减量。
2. 计算执行 20 和 100 CPU 小时后经历的故障数和故障强度。
3. 计算达到 5 个故障/CPU 小时的故障强度目标所需的额外故障数和额外执行时间。

使用基本执行时间模型进行上述计算。

解决方案

(1)当前故障强度

(2)每个故障的故障强度递减量可以计算为

(3)(a) 20 CPU 小时后经历的故障数 & 故障强度

(b)100 CPU 小时后经历的故障数 & 故障强度

4. 达到 5/hr 的故障强度目标所需的额外故障数 (∆μ)。

达到 5/hr 的故障强度目标所需的额外执行时间。