旋转2025年3月17日 | 阅读 3 分钟 它是改变物体角度的过程。 旋转可以是顺时针或逆时针。 对于旋转,我们必须指定旋转角度和旋转点。 旋转点也称为枢轴点。 它是物体旋转的轴心。 旋转类型
枢轴点(旋转角度)的正值使物体沿逆时针方向旋转。 枢轴点(旋转角度)的负值使物体沿顺时针方向旋转。 当物体旋转时,物体的每个点都以相同的角度旋转。 直线: 直线通过端点以相同的角度旋转,并在新端点之间重新绘制该线。 多边形: 多边形通过使用相同的旋转角度移动每个顶点来旋转。 曲线: 曲线通过重新定位所有点并在新位置绘制曲线来旋转。 圆: 可以通过按指定的角度确定中心位置来获得。 椭圆: 其旋转可以通过将椭圆的长轴和短轴旋转到所需的角度来获得。   顺时针方向的旋转矩阵。  逆时针方向的旋转矩阵。  齐次坐标旋转矩阵(顺时针)  齐次坐标旋转矩阵(逆时针)  绕任意点旋转: 如果我们要绕任意点旋转一个物体或点,首先,我们将要旋转的点平移到原点。 然后绕原点旋转点或物体,最后,我们再次将其平移到原来的位置。 我们得到了绕任意点的旋转。 示例: 要旋转点 (x, y) (xc yc) 是执行逆时针旋转的点 步骤1: 将点 (xc yc) 平移到原点 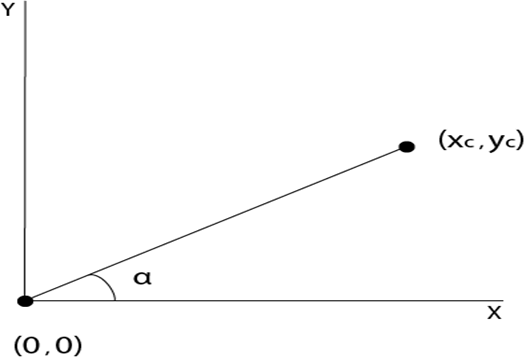 步骤2: (x, y) 绕原点旋转  步骤3: 将旋转中心平移回其原始位置   示例1: 证明绕原点的 2D 旋转是可交换的,即 R1 R2=R2 R1。 解答: R1 和 R2 是旋转矩阵  示例2: 将端点为 (3, 4) 和 (12, 15) 的线 CD 绕原点逆时针旋转 45°。 解答: 点 C (3, 4)    示例3: 将端点为 A (2, 5) 和 B (6, 12) 的线 AB 绕原点顺时针旋转 30°。 解答: 对于顺时针方向的旋转。 矩阵是 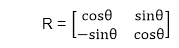 步骤1: 旋转点 A (2, 5)。 取角度 30°  步骤2: 旋转点 B (6, 12)   旋转直线的程序输出 旋转前    旋转后  旋转三角形的程序输出 旋转前   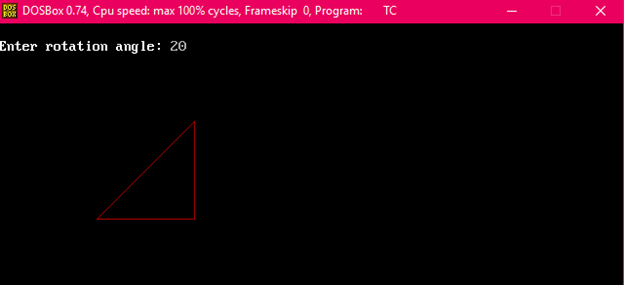 旋转后 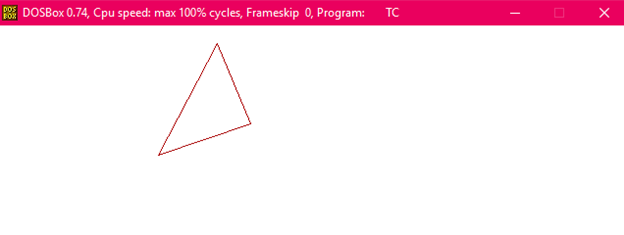 下一主题反射 |
我们请求您订阅我们的新闻通讯以获取最新更新。