布尔函数

布尔代数中使用二元变量和逻辑运算。代数表达式被称为布尔表达式，用于描述布尔函数。布尔表达式由常数值 1 和 0、逻辑运算符号和二元变量组成。

示例 1: F=xy' z+p

我们用四个二元变量 x、y、z 和 p 来定义布尔函数 F=xy' z+p。当 x=1、y=0、z=1 或 z=1 时，此函数将等于 1。

示例 2

输出 Y 在等式的左侧表示。所以，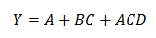

除了代数表达式之外，布尔函数也可以用真值表来描述。我们可以使用多个代数表达式来表示一个函数。它们在逻辑上是等价的。但对于每个函数，我们只有一个唯一的真值表。

在真值表表示中，我们表示所有可能的输入组合及其结果。我们可以将切换方程转换为真值表。

示例：F(A,B,C,D)=A+BC'+D

当 A=1 或 BC'=1 或 D=1 或全部设置为 1 时，输出将为高。 上述示例的真值表如下所示。 2ⁿ 是真值表中行的数量。 n 定义了输入变量的数量。 因此，可能的输入组合是 2³=8。

简化布尔函数的方法

有两种方法可用于简化布尔函数。这些功能如下

卡诺图或 K-map

德摩根定律对于操作逻辑表达式非常有帮助。逻辑门也可以实现逻辑表达式。k-map 方法用于减少逻辑门，以获得实现逻辑表达式所需的最小可能值。K-map 方法将以两种不同的方式完成，我们将在后面的布尔表达式简化部分中讨论。

与非门实现

除了 K-map，我们还可以使用与非门来简化布尔函数。让我们看一个例子

示例 1: F(A,B,C,D)=A' C'+ABCD'+B' C' D+BCD'+A'B'