布尔代数定律和规则

在简化布尔表达式时，布尔代数的定律和规则起着重要作用。在理解这些布尔代数的定律和规则之前，请先理解布尔运算的加法和乘法概念。

布尔加法

布尔代数的加法运算类似于或（OR）运算。在数字电路中，OR运算用于计算和项，而不使用AND运算。 A + B、A + B'、A + B + C' 和 A' + B + + D' 是一些“和项”的示例。当一个或多个文字为真时，和项的值为真；当所有文字都为假时，和项的值为假。

布尔乘法

布尔代数的乘法运算类似于与（AND）运算。在数字电路中，AND运算用于计算乘积，而不使用OR运算。 AB、AB、ABC 和 ABCD 是一些乘积项的示例。当所有文字都为真时，乘积项的值为真；当任何一个文字为假时，乘积项的值为假。

布尔代数定律

布尔代数有以下定律：

交换律

此定律指出，我们使用变量的顺序无关紧要。这意味着变量的顺序不影响结果。在布尔代数中，OR运算和加法运算是相似的。在下图中，OR门显示输入变量的顺序完全无关紧要。

对于两个变量，加法的交换律写为：

对于两个变量，乘法的交换律写为：

结合律

此定律指出，当变量优先级相同时，运算可以按任何顺序进行。例如 '*' 和 '/' 具有相同的优先级。在下图中，结合律应用于 2 输入 OR 门。

对于三个变量，加法的结合律写为：

对于三个变量，乘法的结合律写为：

根据此定律，当对两个或多个变量进行 AND 运算时，变量的组合顺序无关紧要。在下图中，结合律应用于 2 输入 AND 门。

分配律

根据此定律，如果我们对两个或多个变量执行 OR 运算，然后将结果与单个变量执行 AND 运算，则结果将类似于将该单个变量与每个变量执行 AND 运算，然后将该乘积执行 OR 运算。此定律解释了因式分解的过程。

对于三个变量，分配律写为：

布尔代数规则

布尔代数有以下规则，主要用于操作和简化布尔表达式。这些规则在简化布尔表达式中起着重要作用。

规则 1： A + 0 = A

假设；我们有一个输入变量 A，其值是 0 或 1。当我们与 0 执行 OR 运算时，结果将与输入变量相同。因此，如果变量值为 1，则结果为 1；如果变量值为 0，则结果为 0。从图上看，此规则可定义为：

规则 2： (A + 1) = 1

假设；我们有一个输入变量 A，其值是 0 或 1。当我们与 1 执行 OR 运算时，结果将始终为 1。因此，如果变量值是 1 或 0，则结果将始终为 1。从图上看，此规则可定义为：

规则 3： (A.0) = 0

假设；我们有一个输入变量 A，其值是 0 或 1。当我们与 0 执行 AND 运算时，结果将始终为 0。此规则指出，输入变量与 0 进行 AND 运算的结果始终为 0。从图上看，此规则可定义为：

规则 4： (A.1) = A

假设；我们有一个输入变量 A，其值是 0 或 1。当我们与 1 执行 AND 运算时，结果将始终等于输入变量。此规则指出，输入变量与 1 进行 AND 运算的结果始终等于输入变量。从图上看，此规则可定义为：

规则 5： (A + A) = A

假设；我们有一个输入变量 A，其值是 0 或 1。当我们与同一变量执行 OR 运算时，结果将始终等于输入变量。此规则指出，输入变量与其自身进行 OR 运算的结果始终等于输入变量。从图上看，此规则可定义为：

规则 6： (A + A') = 1

假设；我们有一个输入变量 A，其值是 0 或 1。当我们与该变量的补码执行 OR 运算时，结果将始终等于 1。此规则指出，变量与其补码进行 OR 运算的结果始终为 1。从图上看，此规则可定义为：

规则 7： (A.A) = A

假设；我们有一个输入变量 A，其值是 0 或 1。当我们与同一变量执行 AND 运算时，结果将始终等于该变量本身。此规则指出，变量与其自身进行 AND 运算的结果始终等于输入变量。从图上看，此规则可定义为：

规则 8： (A.A') = 0

假设；我们有一个输入变量 A，其值是 0 或 1。当我们与该变量的补码执行 AND 运算时，结果将始终等于 0。此规则指出，变量与其补码进行 AND 运算的结果始终为 0。从图上看，此规则可定义为：

规则 9： A = (A')'

此规则指出，如果我们对变量执行双重取反（两次补码），结果将与原始变量相同。因此，当我们对变量 A 取反时，结果为 A'。进一步，如果我们再次对 A' 取反，我们将得到 A，即原始变量。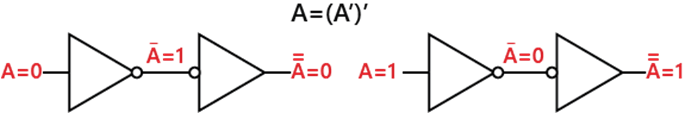

规则 10： (A + AB) = A

我们可以使用规则 2、规则 4 和分配律来证明此规则，如下所示：

规则 11： A + AB = A + B

我们可以使用上述规则来证明此规则，如下所示：

规则 12： (A + B)(A + C) = A + BC

我们可以使用上述规则来证明此规则，如下所示：