卡诺图(K-Map)方法2025年3月17日 | 阅读 3 分钟 K-map 是一种简化布尔表达式的系统方法。借助 K-map 方法,我们可以找到最简单的 POS 和 SOP 表达式,这被称为最小表达式。K-map 提供了一本简化的食谱。 就像真值表一样,K-map 包含输入变量的所有可能值及其对应的输出值。然而,在 K-map 中,这些值存储在数组的单元格中。在每个单元格中,存储每个输入变量的二进制值。 K-map 方法用于包含 2、3、4 和 5 个变量的表达式。对于更多数量的变量,还有另一种用于简化的方法,称为 Quine-McClusky 方法。在 K-map 中,单元格的数量与变量输入组合的总数相似。例如,如果变量的数量是 3,则单元格的数量是 23=8,如果变量的数量是 4,则单元格的数量是 24。K-map 采用 SOP 和 POS 形式。K-map 网格使用 0 和 1 填充。K-map 通过分组来解决。以下步骤用于使用 K-map 求解表达式
2 变量 K-map在 2 变量 K-map 中总共有 4 个变量。2 变量 K-map 中有两个变量。下图显示了 2 变量 K-map 的结构 
3 变量 K-map3 变量 K-map 表示为一个由八个单元格组成的数组。在这种情况下,我们使用 A、B 和 C 作为变量。我们可以使用任何字母作为变量的名称。变量 A 和 B 的二进制值沿左侧排列,而 C 的值沿顶部排列。给定单元格的值是左侧同一行中 A 和 B 的二进制值与同一列中顶部 C 的值的组合。例如,左上角的单元格的二进制值为 000,而右下角的单元格的二进制值为 101。  4 变量卡诺图4 变量 K-map 表示为一个由 16 个单元格组成的数组。变量 A 和 B 的二进制值沿左侧排列,而变量 C 和 D 的值沿顶部排列。给定单元格的值是左侧同一行中 A 和 B 的二进制值与同一列中顶部 C 和 D 的二进制值的组合。例如,右上角的单元格的二进制值为 0010,而右下角的单元格的二进制值为 1010   5 变量 K-map借助 32 单元格 K-map,可以简化具有 5 个变量的布尔表达式。为了构造 5 变量 K-map,我们使用两个 4 变量 K-map。对于 5 变量映射,每个 4 变量映射中的单元邻接性与 4 变量映射相似。 可以使用两个 4 变量映射构造一个用于五个变量 (PQRST) 的 K-map。每个映射包含 16 个单元格,其中包含变量 Q、R、S 和 T 的所有组合。一个映射用于 P = 0,另一个映射用于 P = 1)。 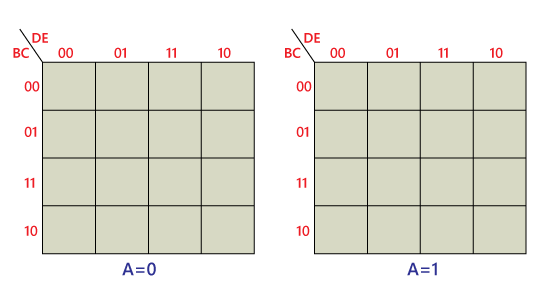 下一主题使用卡诺图简化布尔表达式 |
我们请求您订阅我们的新闻通讯以获取最新更新。