德摩根定理

著名的数学家德摩根发明了布尔代数中两个最重要的定理。德摩根定理用于数学验证 NOR 门和负与门以及负或门和 NAND 门的等价性。这些定理在求解各种布尔代数表达式中起着重要作用。在下表中，定义了输入变量的每个组合的逻辑运算。

德摩根定理的规则由使用两个输入变量 x 和 y 的 或、与和非的布尔表达式产生。德摩根的第一条定理说，如果我们对两个输入变量执行与运算，然后对结果执行非运算，结果将与该变量的补码的或运算相同。德摩根的第二条定理说，如果我们对两个输入变量执行或运算，然后对结果执行 非运算，结果将与该变量的补码的与运算相同。

德摩根第一定理

根据第一个定理，与运算的补码结果等于该变量的补码的或运算。因此，它等同于 NAND 函数，是一个负或函数，证明了 (A.B)' = A'+B'，我们可以使用下表来证明这一点。

德摩根第二定理

根据第二个定理，或运算的补码结果等于该变量的补码的与运算。因此，它等同于 NOR 函数，是一个负与函数，证明了 (A+B)' = A'.B'，我们可以使用以下真值表来证明这一点。

让我们举一些例子，其中我们取一些表达式并应用德摩根定理。

示例 1: (A.B.C)'

(A.B.C)'=A'+B'+C'

示例 2: (A+B+C)'

(A+B+C)'=A'.B'.C

示例 3: ((A+BC')'+D(E+F')')'

要将德摩根定理应用于此表达式，我们必须遵循以下表达式

1) 在完整表达式中，首先，我们找到可以应用德摩根定理的那些项，并将每个项视为单个变量。

所以，

2) 接下来，我们应用德摩根第一定理。所以，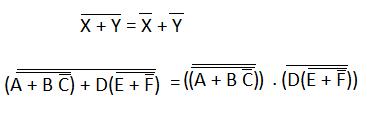

3) 接下来，我们使用规则编号 9，即 (A=(A')') 来取消双杠。

4) 接下来，我们应用德摩根第二定理。所以，

5) 再次应用规则编号 9 来取消双杠

现在，此表达式中没有我们可以应用任何规则或定理的项。所以，这是最终表达式。

示例 3: (AB'.(A + C))'+ A'B.(A + B + C')'