辛普森方法

辛普森法是一种由托马斯·辛普森提出的数值积分方法，因此得名辛普森法。尽管辛普森法有特定的规则，但最基本的有辛普森的两条规则，即：

• 辛普森第一规则：被称为辛普森1/3规则
• 辛普森第二规则：被称为辛普森3/8规则

在本节中，我们将讨论辛普森的这两条规则，并实现这两条规则的示例代码。

辛普森1/3规则

它也被称为辛普森规则，该规则表示：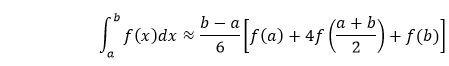

其中f(x)是积分函数，a是下限，b是表达式中的积分上限。

二次插值

用二次多项式P(x)替换积分函数f(x)，P(x)是一条抛物线，它在a和b处取与f(x)相同的值。它还像f(x)一样计算m = (a + b)/2。因此，通过使用拉格朗日多项式插值和代换积分，我们得到：

然后使用步长h=(b-a)/2，它可以写成：

由于它是h/3，即1/3因子，我们称之为辛普森规则为辛普森1/3规则。

辛普森规则可以通过下面的图表推导出来，其中我们用二次插值P(x)近似积分的f(x)。

数值示例

为了解决一个数值问题，我们需要使用辛普森规则，即：

数值问题：在4到5.2的范围内计算logx dx。

解决方案

步骤1：选择将区间划分的值，即n的值。因此，对于给定的表达式，首先我们将区间分成六个相等的部分，因为区间的数量应该是偶数。

步骤2：计算h = (b - a)/2的值

步骤3：评估并计算x₀到x_n的值。考虑y = f(x)并计算x₀到x_n对应的y₀到y_n的值。这里，我们得到以下数据：

步骤3：将值代入方法中，然后我们可以使用上述公式计算积分的近似值。

= h/3[( 1.38 + 1.64) + 4 * (1.43 + 1.52 +

1.60 ) +2 *(1.48 + 1.56)]

= 1.84

因此，使用辛普森1/3规则，上述积分的近似值为1.827。

辛普森1/3规则的程序实现

下面是辛普森1/3规则的C语言程序代码实现：

上述代码的输出如下所示

辛普森3/8规则

它是辛普森的第二条规则，也类似于辛普森1/3规则，但有所不同。1/3规则和3/8规则的区别在于，在辛普森3/8规则中，插值函数是一个三次多项式。辛普森3/8规则表示：

其中f(x)是积分函数，h是区间的长度，计算公式为h = (b - a)/n，其中n是这里的区间限制。

现在，让我们看看程序实现，以理解辛普森3/8规则背后的逻辑。

实现辛普森3/8规则的程序

下面是C++语言的程序代码实现：

上述代码的输出如下所示

除了这些讨论的辛普森的两条规则之外，还存在第三条规则，用于海军建筑和船舶稳定性估算。然而，在一般方法中，它并不重要。