汉诺塔

汉诺塔谜题是一个迷人的挑战，它教会我们宝贵的解决问题技巧和递归思维之美。随着你对它机制的深入了解，掌握这个有趣的谜题的关键在于理解通用规则。

汉诺塔规则

1. 三个柱子：源柱、目标柱和备用柱

汉诺塔谜题的核心是三个柱子，通常标记为A、B和C。每个柱子都可以放置盘子，你的目标是将所有盘子从源柱移动到目标柱，同时使用第三个柱子作为临时存放区域。

2. 盘子大小和堆叠顺序

盘子有不同的尺寸，从底部最大的堆叠到顶部最小的。这种排列至关重要，因为它为谜题的挑战奠定了基础。在整个过程中，你必须始终确保较大的盘子绝不能放在较小的盘子上面。

3. 递归算法

解决汉诺塔谜题的核心策略围绕着一个简单但强大的模式，该模式随着盘子数量“n”而扩展。递归算法如下：

• 将顶部的“n-1”个盘子从源柱移动到备用柱，并以目标柱为中间步骤。
• 将最大的盘子（“n”）从源柱移动到目标柱。
• 将“n-1”个盘子从备用柱移动到目标柱，并以源柱为中间步骤。

4. 理解递归

递归是计算机科学和数学中的一个基本概念。它涉及将复杂问题分解为更简单、相似的子问题。在汉诺塔的背景下，算法会不断地将其应用于较小的子问题，直到达到基本情况，即移动单个盘子，这是一个容易实现的任务。

5. 解决谜题

要解决汉诺塔谜题，请从源柱上初始配置的盘子开始。应用递归算法将盘子从源柱移动到目标柱，并始终遵守规则。当你解决子问题时，谜题会逐渐转变为一组更小、更易于管理的任务。

6. 指数增长之美

汉诺塔谜题的一个有趣方面是，随着盘子数量的增加，所需移动次数的指数增长。对于“n”个盘子，所需的移动次数为2^n - 1。这种快速增长展示了简单规则和复杂结果之间复杂的相互作用。

7. 耐心和策略

虽然汉诺塔谜题的规则很简单，但成功完成它需要耐心和战略性思维。你必须仔细计划你的移动并预测每一步的结果。这个谜题鼓励你去探索各种路径并评估你决策的后果。

这个谜题听起来可能很复杂，但我们可以将其分解为简单的步骤

1. 从一个盘子开始

考虑这个问题的最小版本：只有一个盘子。移动一个盘子是一个非常简单的过程。你将其从源柱拿起，然后放在目标柱上。

2. 两个盘子

现在，想象你有两个盘子，标记为“A”和“B”，堆叠在源柱上。要将这两个盘子移动到目标柱，你必须遵循以下步骤：

• 将盘子“A”从源柱移动到备用柱。
• 将盘子“B”从源柱移动到目标柱。
• 将盘子“A”从备用柱移动到目标柱。

3. 三个盘子

随着盘子数量的增加，谜题变得更加有趣。我们以三个盘子为例：“A”、“B”和“C”。解决方法如下：

• 首先，使用目标柱作为中间步骤，将顶部的两个盘子（“A”和“B”）移动到备用柱。这遵循我们用于两个盘子的相同步骤。
• 现在，将最大的盘子（“C”）移动到目标柱。
• 最后，使用源柱作为中间步骤，将两个较小的盘子（“A”和“B”）从备用柱移动到目标柱。

4. 四个盘子

当你添加更多盘子时，模式会继续。对于四个盘子（“A”、“B”、“C”和“D”），过程如下：

• 使用目标柱作为中间步骤，将顶部的三个盘子（“A”、“B”和“C”）移动到备用柱。
• 将最大的盘子（“D”）移动到目标柱。
• 使用源柱作为中间步骤，将三个较小的盘子（“A”、“B”和“C”）从备用柱移动到目标柱。

示例

我们以一个程序为例来说明具有三个柱子的汉诺塔问题

输出

说明

递归的工作原理

假设你有一个盘子堆，你想将它们从一个柱子移动到另一个柱子，并有一个备用柱用于临时存放。如果你只有一个盘子，那很简单；你只需直接移动它。但如果你有多个盘子，递归的魔力就会显现。

如果你想移动n 个盘子，你首先将顶部的n-1 个盘子从源柱移动到备用柱（使用目标柱作为临时存储）。这会腾出最底部的盘子，然后你可以将其直接移动到目标柱。之后，你将n-1 个盘子从备用柱移动到目标柱，并使用源柱作为临时存储。这就像解决同一问题的较小版本两次，一次是为了给最大的盘子清路，一次是将其余盘子移到目标柱。这个过程会为每个较小的子问题不断重复，直到你达到移动单个盘子的基本情况，这很简单。递归的优点是每个子问题都使用相同的方法来解决，使得解决方案优雅且易于理解。

程序中的变量

n：要移动的盘子数量。

source：从中移动盘子的源柱。

auxiliary：用于临时存储的辅助柱。

destination：要将盘子移动到的目标柱。

示例

我们以一个程序为例来说明具有五个柱子的汉诺塔问题

输出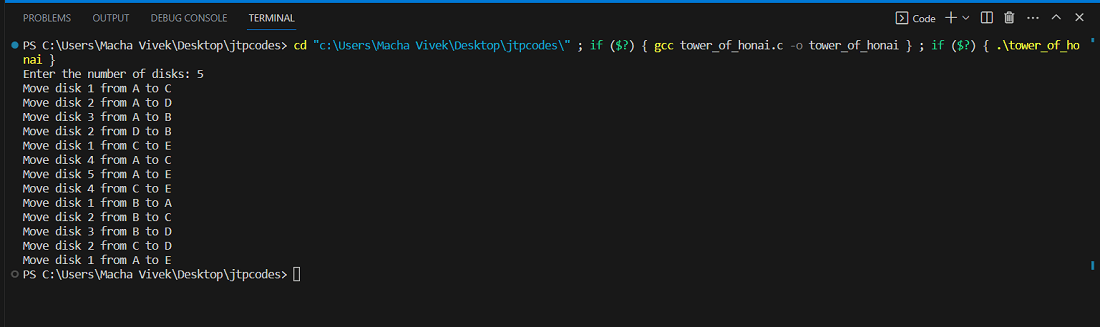

说明

在传统的汉诺塔问题中，你有三个柱子（我们称之为A、B和C），目标是将一叠盘子从A 柱移动到C 柱，并遵守某些规则。将其扩展到五个柱子会增加额外的复杂性。

在五柱汉诺塔问题中，你仍需遵循一系列规则：

• 一次只能移动一个盘子。
• 较大的盘子不能放在较小的盘子上面。
• 你有五个柱子而不是三个，你需要将整个堆栈从一个柱子（源柱）移动到另一个柱子（目标柱），并使用剩余的柱子作为临时存储。

你可以使用类似的递归方法来解决这个扩展的问题，但这会变得更加复杂。以下是该方法的高层解释：

基本情况：当只有一个盘子时，你可以将其直接从源柱移动到目标柱。

递归步骤：当有多个盘子时，你需要将问题分解为更小的子问题。如果你想使用五个柱子将n 个盘子从源柱移动到目标柱，你可以这样做：

• 将顶部的 n-2 个盘子移动到一个辅助柱。
• 将第 (n-1) 个盘子移动到另一个辅助柱。
• 将第 n 个盘子移动到目标柱。
• 将第 (n-1) 个盘子从辅助柱移动到目标柱。
• 将n-2 个盘子从第一个辅助柱移动到目标柱。

递归：对子问题递归地应用相同的策略。这个过程一直持续到达到移动单个盘子的基本情况。

将汉诺塔问题扩展到五个柱子的关键挑战在于跟踪要用作辅助柱的柱子，并确保遵守问题规则。递归方法通过解决问题的较小实例并组合它们的解决方案来移动整个盘子堆，从而帮助管理这些复杂性。