C 语言斯特恩-布罗科特数列

在本文中，我们将讨论 C 语言中的 Stern-Brocot 序列，包括其算法、示例和优点。

什么是 Stern-Brocot 序列？

Stern-Brocot 序列，通常称为 Stern 二进制级数，是通过以下方式生成的数字序列。

• 例如：1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, ...
• 尽管斐波那契数列和 Stern-Brocot 序列之间有许多相似之处，但 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,...
• Stern-Brocot 序列和斐波那契数列是通过不同的过程生成的。在斐波那契数列中，每个数字等于它前面的两个数字的总和。斐波那契数列规则规定，序列中的每个数字都等于它前面的两个数字的总和。一些例子是 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13，依此类推。
• 在 Stern-Brocot 序列中，与斐波那契数列不同，我们考虑的不仅仅是数字的总和。

问题陈述

实现一个程序在 C 语言中打印 Stern-Brocot 序列。

说明

• 序列的第一部分和第二部分是 1：[1, 1]。
• 现在让我们检查一下序列的第二部分。
• 将序列中考虑的元素与其前面的元素相加，然后将其附加到序列的末尾（例如，1 + 1 = 2）。
• [1, 1, 2].
• 接下来，将序列中评估的元素放在序列的末尾：[1, 1, 2, 1]。
• 选择序列中的第二个元素。
• 将其与前面的元素相加（2+1=3），然后将其放在序列的末尾。
• [1, 1, 2, 1, 3].
• 请将此添加到序列的末尾：[1, 1, 2, 1, 3, 2]。
• 接下来要考虑的是第四个元素（即 1）。
• 将其与前面的元素相加（1+2=3），然后将其放在序列的末尾。
• [1, 2, 3, 1, 1, 2, 3, 2, 3].
• 请将此添加到序列的末尾：[1, 1, 2, 1, 3, 2, 3, 1]。
• 这就是顺序的延续：第五个元素，即 3，是接下来要考虑的。
• 因此，序列如下：1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, ...。

算法

步骤 1： 开始。

步骤 2： 定义 n1=1, n2=1, n3, i 和 number。

步骤 3： 为 number 赋值。

步骤 4： 运行循环。

步骤 5： 将 n1 和 n2 相加，并将结果赋值给 n3。

步骤 6： 打印 n3 和 n2。

步骤 7： 更新 n1 和 n2 的值。

步骤 8： 继续循环直到停止。

步骤 9： 停止。

示例 1

让我们举一个例子来说明 C 语言中的 Stern-Brocot Sequence 。

输出

说明

1. 初始化： 在此示例中，n1 和 n2 初始化为 1。这对应于序列的起始元素。
2. 循环： 循环从 2 开始，因为前两个元素已经打印。循环一直运行到 i 小于 number（在本例中为 9）。
3. 序列生成： 在循环内部，n3 计算为 n1 和 n2 的总和，这是序列中的下一个元素。
4. 打印： 打印下一个项 n3。
5. 更新： 更新 n1 和 n2 以继续处理序列中的下一项。

示例 2

让我们再举一个例子来说明 C 语言中的 Stern-Brocot Sequence 。

输出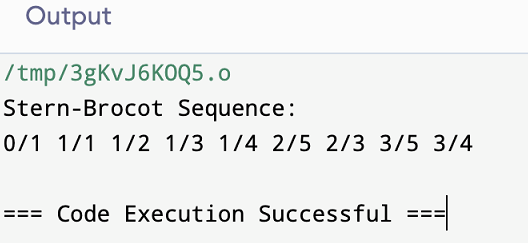

说明

1. sternBrocot 函数： 在此示例中，此函数接收两个由 (num1, den1) 和 (num2, den2) 表示的分数，以及递归的当前深度。

• 基本情况： 如果深度为 0，则函数返回而不执行任何操作。
• 中值计算： 两个分数 num1/den1 和 num2/den2 的中值计算为 (num1 + num2) / (den1 + den2)。
• 打印中值： 打印中值。
• 递归调用： 函数递归调用自身以生成 Stern-Brocot 树的左分支和右分支。

2. main 函数

• 深度： 在此示例中，深度设置为 3，但可以更改它以生成更深或更浅的序列。
• 打印初始项： 打印初始项 0/1 和 1/1。
• 递归生成： 调用 sternBrocot 函数，传入初始项和指定的深度。

此代码将打印指定深度的 Stern-Brocot 序列。调整 depth 变量以控制生成序列的级别数。例如，将 depth = 3 将打印深度为三级的序列。

Stern-Brocot 序列的优点。

Stern-Brocot 序列以 **Moritz Stern ** 和 **Achille Brocot ** 的名字命名，是一个具有多种显著特性和应用的数学序列。以下是 Stern-Brocot 序列的一些优点和用途：

1. 分数生成： Stern-Brocot 序列精确地生成所有正有理数，且每个分数都以最简形式出现且仅出现一次。它的这种属性使其在许多涉及分数和有理数的研究中非常有用。
2. 中值属性： Stern-Brocot 序列中相邻两个项的中值位于它们之间。当使用介于两个给定分数之间的一个更简分数来表示有理数时，此属性在近似分数方面非常有用。
3. 二叉搜索树： 该序列用于生成 Stern-Brocot 树，该树为每个分数创建一个节点，从而形成一棵二叉搜索树。这种树结构简化了许多操作，例如分数的加法、减法、乘法和除法。
4. 连续分数近似的有效性： 利用连续分数近似实数是一种有价值的方法，这得益于 Stern-Brocot 序列。与十进制分数相比，连续分数提供了实数更精确的表示，并在各种数学和计算应用中有用。
5. Farey 序列： Farey 序列考虑 0 到 1 之间所有不重复的、不可约的、分母小于或等于给定界限的分数。Stern-Brocot 序列可以看作是 Farey 序列的一个特定实例。理解 Stern-Brocot 序列的属性有助于我们理解 Farey 序列的属性。
6. 数论和丢番图方程： Stern-Brocot 序列的性质在数论中很有用，尤其是在研究有理数上的丢番图方程时。该序列阐明了有理数的性质和构成。
7. 格点和几何： 几何学与 Stern-Brocot 序列相关，特别是在理解格点和有理数的几何配置方面。这些相互作用影响了数学的许多领域，包括几何、数论和组合学。