Python中的凝聚层次聚类2025年1月5日 | 阅读 7 分钟 在信息分析、机器学习和数据挖掘领域,层次聚类是一种强大而适应性强的技术。它是对相似数据点进行聚类的广泛使用的方法,这使其成为图像处理、生物学、社会科学和金融等许多领域的重要工具。  通过根据相似性对数据点进行聚类,这种称为层次凝聚聚类的方法会创建数据的层次表示。 与 K-均值等其他聚类方法不同,层次聚类不需要用户预先确定簇的数量。相反,它会生成一个树状图,这是一个树状结构,其中每个数据点最初都是一个单独的簇,并根据相似性与其他簇合并,最终形成一个层次结构。 层次聚类的关键概念
层次聚类的优点
层次聚类的应用
挑战与注意事项
凝聚层次聚类凝聚层次聚类是最流行的聚类方法之一。它遵循“自下而上”的方法,从每个数据点作为一个单独的簇开始,然后逐步合并这些簇,直到只剩下一个。结果是一个层次结构,通常表示为树状图,它直观地说明了数据点之间的聚类关系。过程一直持续到达到所需的簇数或满足某个停止条件为止。 距离度量层次聚类的核心是距离度量的概念。这些度量量化数据点之间的相似性或不相似性。常见的距离度量包括欧几里得距离、曼哈顿距离和各种链接方法。距离度量的选择可能显著影响聚类结果。 链接方法链接方法决定了在凝聚过程的每一步如何合并簇。不同的链接方法具有不同的合并簇的标准。一些常见的链接方法包括:
链接方法的选择会影响簇的形状和质量。 凝聚聚类过程凝聚层次聚类过程可分为以下步骤:
树状图树状图是层次聚类过程的可视化表示。它看起来像一棵树状图,数据点是叶子,簇是内部节点。树状图中每个分支的高度代表簇或数据点之间的不相似性。通过在特定高度切割树状图,您可以获得不同数量的簇。在层次聚类中,在哪里切割树状图的选择是一个关键决定。 簇的数量确定合适的簇数量是层次聚类中的一个关键步骤。此决定可以基于领域知识、树状图的结构或定量方法,例如肘部法则。肘部法则涉及观察簇内方差随着簇数量的增加如何减小。“肘部”点在图上表示最佳簇数量。 凝聚层次聚类的应用凝聚层次聚类广泛应用于生物学、社会科学、营销和图像分析等各个领域。在生物学中,它可以帮助根据遗传数据对物种进行分类。在营销中,它可以对客户进行细分以进行定向广告。在图像分析中,它可以对相似图像进行分组以进行基于内容的检索。 凝聚层次聚类的优点凝聚层次聚类具有以下优点:
挑战与注意事项尽管有其优点,凝聚层次聚类仍存在一些挑战和考虑因素:
总之,凝聚层次聚类是一种多功能的聚类方法,它创建一个簇的层次结构,从而能够对数据的分组进行详细或粗粒度的洞察。它依赖于距离度量和链接方法来迭代地合并簇。其可视化表示树状图有助于理解聚类关系。这项技术在各个领域都有应用,并在可解释性和灵活性方面提供了优势,但它也带来了与计算复杂性和对噪声的敏感性相关的挑战。当深思熟虑地应用并使用正确的参数时,凝聚层次聚类可以为复杂数据集提供宝贵的见解。 源代码 输出 1. 代表凝聚层次聚类的图  2. 代表树状图的图 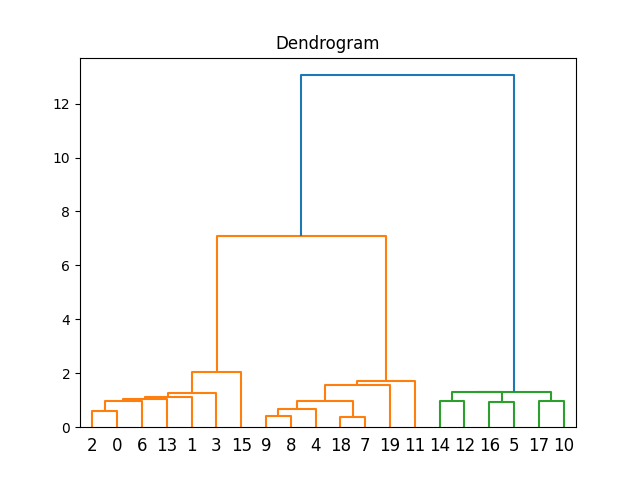 |
t-分布随机邻域嵌入 (t-SNE) 一种名为 T-分布随机邻域嵌入 (t-SNE) 的非线性降维方法是理想的。什么是降维?在二维或三维中,n 维数据(具有多个特征的多维数据)由降维表示。分类问题,例如学生是否会踢足球……
7 分钟阅读
计算机科学领域最基本的数据结构,不相交集,也称为 Union-Find 方法,可以有效地处理将组件分割成不相交集的问题。当处理涉及连接性和等价性关系的问题时,这种方法非常有用……
阅读 6 分钟
? Pandas 是一个强大的 Python 库,广泛用于数据操作和分析。处理数据时的一项常见任务是重命名 DataFrame 中的列标题。虽然重命名单个列很简单,但重命名多个列标题需要更系统的方法。在这...
5 分钟阅读
在 Python 中,比较运算符用于使用运算符(如“<”表示小于,“>”表示大于或“==”表示等于)来比较两个值。它也称为关系运算符。您甚至可以使用运算符...
阅读 6 分钟
?在Linux系统中,需要检查特定内容是否正在运行的情况并不少见。这对于各种目的都很有用,例如监控、确保单实例执行或根据内容的状况执行活动。Python提供了多种方式...
阅读 6 分钟
介绍 Python 中的邻域变量在特性内部被描述,并且只能在该特性内部访问。在调用该特性后,它会被创建,并在该特性结束后被销毁。特性体内的变量,...
阅读 6 分钟
简介 试位法,通常称为 Regula Falsi 法,是一种用于求解非线性方程的数值方法。但当根位于特定区间时,该方法特别有效。在这里,我们将深入探讨 False 的基础...
5 分钟阅读
翻转一个有偏硬币提供了一种有趣的方式来找到概率交集理论和编程。与公平硬币(其中出现正面或反面的可能性相同,即 50-50)不同,在有偏硬币中,每个硬币都有一个固定的、不相等的可能性...
阅读 6 分钟
简介:在本教程中,我们将学习 PATCH 方法 - Python requests。request 函数库是 Python 中用于向 URL 发出 HTTP 请求的重要组成部分。本文解释了如何使用 requests.patch() 方法向 URL 请求 PATCH ……
阅读 3 分钟
Twitch Planet 提供绝对巨大的流媒体功能,如果您是开发人员或内容创建者,您可能希望将 Twitch 的 API 集成到您的 Python 项目中。此 API 提供 Twitch 提供的所有功能,从流详细信息到用户...
阅读 4 分钟
我们请求您订阅我们的新闻通讯以获取最新更新。

我们提供所有技术(如 Java 教程、Android、Java 框架)的教程和面试问题
G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India
