Python中中国剩余定理的实现（模逆实现）

引言

CRT 是一个数学概念，用于解决模同余系统。它常用于数论和密码学中进行快速模运算计算。在本文中，我们将讨论使用 Python 中的模逆元方法实现中国剩余定理的应用。

什么是 CRT？

CRT 是一个数学定理，用于解决形式的同余方程组。它引入了一种方法，可以唯一地获得一个数，该数在除以几个成对互质整数时的余数是已知的。这意味着中国剩余定理计算同余方程组的解，从而根据其残差得出未知的整数。

公式

如果给定成对相对素同余方程组 (x) 的形式，CRT 会给出一个公式来求解 x mod M。如果我们有一组方程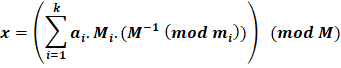

其中

• M=m₁.m₂....m_k 是所有模的乘积。
• 是除 之外所有模的乘积。
• M_i^-1 是 M_i 模 m_i 的模乘法逆元。

当相关的模互质时，该公式可以有效地找到模 M 的解 x。

Python 代码实现

让我们看一下中国剩余定理的实现。

输出

X is 41

说明

• Python3 程序说明了中国剩余定理，这是一个用于模同余方程组的数学概念。提供的代码包含两个主要函数：'inv' 和 'findMinX'。
• 'Inv' 函数使用扩展欧几里得算法计算数字 'a' 关于 'm' 的模逆元。它声明变量，并实现一个确保结果为正的算法。
• 'findMinX' 函数计算满足一组模同余方程的最小数字 'x'。此函数接收数组，其中 num 和 rem 分别是模和余数；k - 同余方程的数量。该函数将所有模的值相乘，并反复应用 CRT，CRT 使用由 inv 计算的逆值。
• 在提供的示例中，程序解决了以下同余方程组：X=2(mod3)，x=3(mod4)，X=1(mod5)。结果显示在 print("x is", findMinX(num, rem, k)) 输出中，表示此实例的 x 的答案。

结论

对 CRT 及其 Python 版本的分析表明，这种数学方法可以高速解决模同余方程组。此代码表示反映了 CRT 在 inv 和 findMinX 函数中的实际表达，从而证明了其有用性。该实现作为模逆元和 CRT 公式计算的描述，并加以强调。应将这些数学原理理解为正确应用 CRT 在数论和密码学等多个领域中不可或缺的一部分。该代码不仅揭示了 CRT 的魅力，还为那些希望使用其计算来应用该定理的人提供了一个起点。