Python中的高斯拟合

什么是高斯分布或正态分布？

当我们绘制数据集（例如直方图）时显示的形状被称为其分布。钟形曲线，也称为高斯分布或正态分布，是最常观察到的连续值形状。

它以德国数学家卡尔·弗里德里希·高斯的名字命名。智商分数、体温、个人身高和汽车里程是符合高斯分布的几个典型数据集示例。

让我们尝试使用 Python 创建最佳正态分布并绘制它。

如何使用 Python 绘制高斯分布？

为了帮助我们创建最佳的正态曲线，有 NumPy、SciPy 和 Matplotlib 等库可用。

代码

程序说明

附带的 Python 脚本使用 NumPy、SciPy 和 Matplotlib 库构建并可视化了一个理想化的典型曲线。它包括 numpy.linspace 在 -5 到 5 的范围内创建 x 轴值，stats.norm.pdf 基于高斯分布计算相等的 y 轴值，以及 Matplotlib 来绘制曲线。均值为 0，标准差为 1，生成的图描绘了一个标准的典型分布。通过 plt.show() 命令显示该图。

输出

x 轴上的点代表观测值，y 轴显示每个观测值的概率。

使用 np.arange()，我们在 (-5, 5) 范围内生成了等距的观测值。接下来，我们将其通过标准。使用均值为 0.0 且标准差为 1 的 pdf() 函数生成了该特定观测值的概率。最常见的观测值是 0 附近的，而最稀有的观测值是 -5.0 和 5.0 附近的。概率密度函数是 pdf() 函数的专业名称。

高斯函数

拟合数据的第一步是拟合高斯函数。我们的目标是找到最适合我们数据的 A 和 B 的值。首先必须将高斯函数方程写成一个 Python 函数。它应该接受构成该函数的所有参数以及自变量（x 值）。

为了拟合我们的数据，我们将使用 Python 模块 scipy.optimize 中的 curve_fit 函数。它使用非线性最小二乘法将数据拟合到有用的形状。请使用 Jupyter Notebook 中的帮助功能或 Scipy 在线手册了解更多关于 curve_fit 的信息。

curve_fit 函数的三个必需输入是您要拟合的函数、x 数据和 y 数据。有两个输出。第一个是参数的最佳值范围。第二个是参数估计协方差的矩阵，可以从中计算出参数的标准误差。

示例 1

程序说明

此 Python 软件使用 NumPy、Matplotlib 和 SciPy 模块将高斯函数应用于一组数据点。首先绘制信息点，然后定义 x 和 y 数据簇以及高斯函数。为了确保最佳数据拟合，SciPy curve_fit 函数最大化高斯函数的参数。通过绘制与原始数据进行简单视觉比较的生成曲线，生成了在预定义数据范围内拟合的高斯函数图。

输出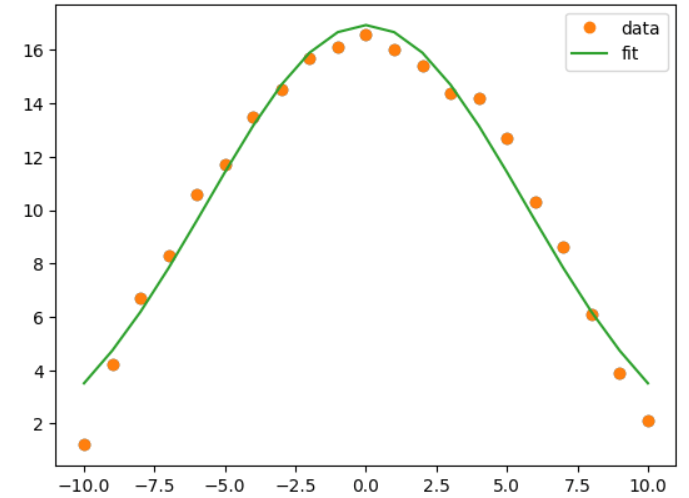

示例 2

程序说明

此 Python 软件使用 SciPy、NumPy 和 Matplotlib 将高斯函数拟合到带噪数据。定义一个高斯函数，生成干净的数据，添加噪声以生成带噪数据集，并可视化原始函数和带噪数据。为了最好地拟合带噪数据，curve_fit 函数优化了高斯函数的参数。之后，脚本绘制带噪数据、原始函数和最佳拟合曲线，并将图保存为“model_fit.png”，并输出最佳拟合参数。此过程演示了在带噪实验数据上使用高斯模型进行曲线拟合和参数估计的方法。

输出