人工智能中的手段-目标分析

2025年5月6日 | 阅读 6 分钟

我们已经学习了可以正向或反向推理的策略，但对于解决复杂而庞大的问题，混合使用这两种方向是更合适的。这种混合策略可以先解决问题的主要部分，然后再回头解决在组合大问题时出现的小问题。这种技术被称为手段-目标分析。

手段-目标分析 (Means-Ends Analysis) 是一种用于限制人工智能程序搜索的问题解决技术。它是反向和正向搜索技术的混合。MEA 技术最初于 1961 年由 Allen Newell 和 Herbert A. Simon 在他们名为 General Problem Solver (GPS) 的问题解决计算机程序中引入。MEA 分析过程着重于评估当前状态和目标状态之间的差异。

手段-目标分析如何工作？

手段-目标分析过程可以递归地应用于一个问题。这是一种控制问题解决搜索的策略。以下是描述 MEA 技术解决问题工作方式的主要步骤：

首先，评估初始状态和最终状态之间的差异。
为每个差异选择可以应用的各种算子。
在每个差异处应用算子，以减小当前状态和目标状态之间的差异。

算子子目标

在 MEA 过程中，我们检测当前状态和目标状态之间的差异。一旦出现这些差异，我们就可以应用算子来减小差异。但有时算子可能无法应用于当前状态。因此，我们为当前状态创建一个子问题，在该子问题中可以应用算子。这种通过反向链接选择算子，然后设置子目标来满足算子先决条件的类型称为算子子目标。

手段-目标分析算法

我们设当前状态为 CURRENT，目标状态为 GOAL，则 MEA 算法的步骤如下：

步骤 1： 比较 CURRENT 和 GOAL，如果两者之间没有差异，则返回成功并退出。
步骤 2： 否则，选择最显著的差异，并通过执行以下步骤来减小该差异，直到发生成功或失败。
1. 选择一个适用于当前差异的新算子 O，如果没有这样的算子，则发出失败信号。
2. 尝试将算子 O 应用于 CURRENT。创建两个状态的描述。
  i) O-Start，一个 O 的先决条件得到满足的状态。
  ii) O-Result，如果 O 在 O-Start 中被应用所产生状态。
3. If
  (First-Part <------ MEA (CURRENT, O-START)
  和
  (LAST-Part <----- MEA (O-Result, GOAL)，如果成功，则发出成功信号并返回组合 FIRST-PART、O 和 LAST-PART 的结果。

上述算法更适合简单问题，对于解决复杂问题则不够充分。

手段-目标分析示例

让我们看一个例子，其中我们知道初始状态和目标状态如下。在此问题中，我们需要通过查找初始状态和目标状态之间的差异并应用算子来达到目标状态。

解决方案

为了解决上述问题，我们将首先找到初始状态和目标状态之间的差异，然后为每个差异生成一个新状态并应用算子。此问题中的算子是：

移动
删除
展开

1. 评估初始状态： 在第一步中，我们将评估初始状态，并将其与目标状态进行比较，以找出两者之间的差异。

2. 应用删除算子： 我们可以看到第一个差异是目标状态中没有点符号，而初始状态中有，所以，我们首先应用 **删除算子** 来移除这个点。

3. 应用移动算子： 应用删除算子后，出现了一个新状态，我们将再次将其与目标状态进行比较。比较这些状态后，还有一个差异，即正方形在圆的外面，所以，我们将应用 **移动算子**。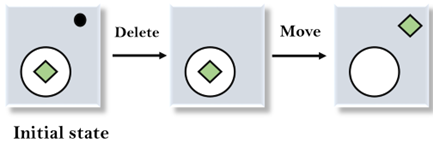

4. 应用扩展算子： 现在在第三步中生成了一个新状态，我们将此状态与目标状态进行比较。比较状态后，仍然存在一个差异，即正方形的大小，因此，我们将应用 **扩展算子**，最终，它将生成目标状态。

手段-目标分析的用途

人工智能 (AI) 系统通常采用手段-目标分析。由于分析中涉及的计算过程模仿了人类认知和解决问题能力的某些特征，因此它是开发像人类一样行为的 AI 系统中的一项关键的基于目标的解决问题技术。通过结合反向和正向搜索策略，AI 系统还采用手段-目标分析，通过评估问题当前状态与期望状态之间的差异来限制程序内的搜索。

实施

现在，我们将通过应用加、减或乘等运算来模拟从起始数字到目标数字的移动，这将有助于理解 MEA。

代码

# Importing libraries
import networkx as nx
import matplotlib.pyplot as plt
import time

# basic graph function
def createMyGraph():
    g = nx.Graph()
    
    # These are the places (nodes)
    placeNames = ['Start', 'point_A', 'point_B', 'point_C', 'point_D', 'point_E', 'Goal']
    for p in placeNames:
        g.add_node(p)
        
    # now putting the roads (edges) with distances
    g.add_weighted_edges_from([
        ('Start', 'point_A', 2),
        ('Start', 'point_B', 4),
        ('point_A', 'point_C', 2),
        ('point_B', 'point_D', 1),
        ('point_C', 'point_E', 3),
        ('point_D', 'point_E', 1),
        ('point_E', 'Goal', 2)
    ])
    
    return g

# used to find how far a node is from the goal
def distanceGuess(graphx, frm, to):
    try:
        dist = nx.shortest_path_length(graphx, frm, to, weight='weight')
    except:
        dist = float('inf')
    return dist

# The actual means-end logic goes here
def meaSolver(grph, st, gl):
    cur = st
    trail = [cur]
    counter = 0

    print("=== STARTING MEA ===\n")

    while cur != gl:
        neigh = list(grph.neighbors(cur))
        best = None
        bestH = float('inf')
        
        for x in neigh:
            guess = distanceGuess(grph, x, gl)
            if guess < bestH:
                best = x
                bestH = guess

        if best is None:
            print("No more moves :(")
            return trail
        
        print(f"Move {counter+1}: {cur} -> {best} (h={bestH})")
        cur = best
        trail.append(cur)
        showGraph(grph, trail, cur, gl, counter)
        time.sleep(1)
        counter += 1

    print("\nReached the goal ")
    return trail

# This draws the graph at each step
def showGraph(g, visited, now, goal, stepN):
    pos = nx.spring_layout(g, seed=1)
    plt.figure(figsize=(8,6))
    nx.draw(g, pos, with_labels=True, node_size=700, node_color='lightblue', edge_color='grey')

    nx.draw_networkx_nodes(g, pos, nodelist=[now], node_color='orange', node_size=800)
    nx.draw_networkx_nodes(g, pos, nodelist=[goal], node_color='green', node_size=800)

    # show path so far
    path_edges = list(zip(visited[:-1], visited[1:]))
    nx.draw_networkx_edges(g, pos, edgelist=path_edges, edge_color='blue', width=2)

    labels = nx.get_edge_attributes(g, 'weight')
    nx.draw_networkx_edge_labels(g, pos, edge_labels=labels)

    plt.title(f"Step {stepN+1}: at {now}")
    plt.axis('off')
    plt.pause(1)
    plt.close()

# running it
myG = createMyGraph()
res = meaSolver(myG, 'Start', 'Goal')

print("\nFinal Path:")
for i, pt in enumerate(res):
    print(f"{i+1}: {pt}")
<textarea>

输出

移动 1： Start -> point_B (h=4)

移动 2： point_B -> point_D (h=3)

移动 3： point_D -> point_E (h=2)

移动 4： point_E -> Goal (h=0)

Reached the goal
Final Path:
1: Start
2: point_B
3: point_D
4: point_E
5: Goal

算法从标记为“Start”的节点开始，在每一步分析所有附近的节点，并根据估计的最短路径（启发式）选择似乎最接近目标的节点。在给定的例子中，路径是 Start-> point_A->point_C-> point_E-> Goal。这表明代理程序始终选择了预期剩余成本最低的方向，从而系统地缩小了与目标的差距。该图通过突出显示的每次移动，可以轻松观察决策过程。

下一主题AI 中的对抗搜索