人工智能中的井字棋问题

井字棋（Tic Tac Toe）是一个简单而有趣的游戏，使其成为研究人工智能在博弈论中能力的理想平台。这个游戏很简单，由两名玩家轮流在一个 3x3 的棋盘上放置自己的标记，目标是将自己的三个标记连成横、竖或斜线。尽管看起来简单，井字棋却引发了人工智能中的一些基本概念，如决策选择、策略制定和对手预测；这使得它成为所有想要投身人工智能、博弈论和算法开发领域的开发者和研究人员的一个很好的入门选择。

井字棋问题的本质在于找到一个玩家可以采用的最佳策略来获胜，或者至少不输。因为棋盘状态的数量是有限的——不超过 9!——所以人工智能系统完全有可能检查所有可能的结果，并在每一步选择最佳走法。这意味着人工智能必须像人类智能一样行事，根据棋盘的状态、对对手走法的预期以及策略的调整来做出有效决策。

代码

现在，为了更好地理解，我们将实现一个玩井字棋游戏的模型。

导入库

创建一个井字棋游戏

首先，我们必须实现游戏本身，才能学习如何玩井字棋。Numpy 是 Python 中用于数值计算最有用的库之一。我们可以很容易地实现一个简单的游戏。在这个 Numpy 数组中，我们将游戏棋盘表示为一个 3x3 的 Numpy 数组。它使用一种特定的表示法：2 代表无人占用的格子，换句话说，代表一个空格子，0 代表“O”，1 代表“X”。默认情况下，数组用数字 2 填充。这意味着棋盘上所有位置最初都是空的。在这个 Numpy 数组中，玩家轮流选择坐标，放置他们各自的标记——0 或 1。基本上，每个玩家的获胜条件是在横、竖或斜线上有三个自己的标记。为简化实现，程序将始终使用标记 1（“X”），而对手将使用标记 0（“O”）。这种直接方法旨在专注于游戏机制，并为教会程序如何制定策略和有效游戏建立一个基础。

下面是一张图，让你熟悉 Numpy 井字棋棋盘

测试井字棋游戏

现在我们将进行一些虚拟对局来测试上面创建的井字棋游戏。我们需要为每个玩家走一步。

输出

生成合法走法

合法走法生成器是一个函数，它接收棋盘状态和玩家作为输入，返回所有可能的合法走法的集合。

更直观地说，给定棋盘状态和一名玩家，它会告诉我们玩家可以在哪里放置他的标记——也就是那些没有对手标记的地方。

测试合法走法

现在让我们来测试上面创建的合法走法生成器。

我们开始一个虚拟游戏并掷硬币决定先后手。然后，我们将当前的棋盘状态和掷硬币的获胜者传递给合法走法生成器。它会返回一个合法走法的字典。这个字典的格式是“可能的下一个合法走法坐标”：“扁平化后的结果棋盘状态”。

输出

我们可以注意到，上面合法走法生成器的返回值是一个字典，包含了所有可能的合法坐标及其对应的扁平化后的 numpy 棋盘状态。

神经网络模型

这是将要完成这项工作的模型，其中的评估器函数将棋盘状态映射到分数。

输出

程序走法选择器

程序走法选择器在给定当前棋盘状态的情况下，以非常有条理的方式为玩家选择下一步。它首先依赖合法走法生成器来生成所有可从当前配置派生出的合法棋盘状态。生成了下一组可能的棋盘状态后，它会借助评估器为这些状态中的每一个打分。评分基于几个因素；综合起来，它们评估了每个棋盘状态的优劣。然后，评估器得分最高的棋盘状态被选为下一步。通过这种方式，可以保证所选的走法既是合法的，又是根据模型的评估标准具有策略性的。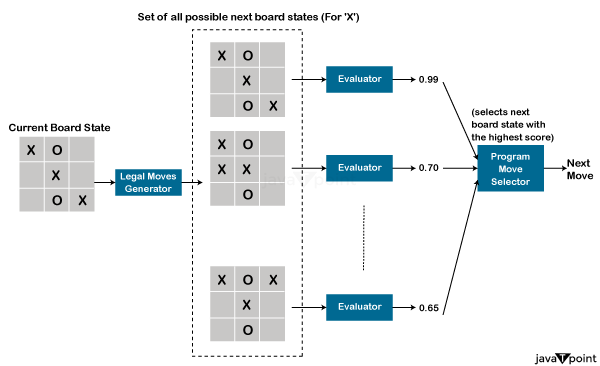

测试程序选择器

现在，让我们用程序走法选择器函数来模拟一场井字棋游戏，由它选择下一步。我们将经历游戏中的几个步骤，以展示该函数如何根据给定的算法评估棋盘状态来选择最优走法。

输出

目前，模型评估器还没有经过训练，因此这些权重是随机的，这使得上面的分数是一个随机数。

对手的走法

井字棋的问题在于它太简单了，这通常会使游戏变得重复。在玩了大约 10-15 局游戏后，我们注意到程序和它的对手会陷入一种重复走法的模式，因为它们都遵循类似的模型。这种缺乏变化是井字棋的一个显著局限性。然而，像跳棋这样的游戏，由于其额外的可变性和策略深度，会使学习过程更具挑战性。在这样的设置中，为了学习，一个程序会与一个编码的对手对战，该对手被设计来模拟不同级别的难度。这个对手会根据所选模式改变其行为。例如，在简单模式下，对手会采用非常简单的方法。在对手的回合，它会使用合法走法生成器生成棋盘上所有可能的合法走法。然后，它会随机选择其中一步，并一直这样玩到游戏结束。通过这个过程，程序可以在不经常遇到非常困难的策略性情况的情况下进行大量运行，并能够广泛地探索井字棋的状态空间。

然而，困难模式下的对手遵循一种更具策略性的方法。首先，它运行一个合法走法生成器，告诉它所有可能的合法走法。如果有任何一步可以通过完成一行、一列或一对角线而立即获胜，那么对手就会选择这一步。如果对手没有找到能赢的走法，它会寻找能够阻止程序在下一回合获胜的走法。这是一种试图切断程序进展的防守策略。此外，如果存在一个合法的走法，可以产生一个包含两个“0”且不包含“1”的行、列或对角线配置，对手会选择这一步。如果这些条件都不满足，它就会随机选择一步。这种进攻和防守走法的混合，造就了一个更现实、更可信的对手，程序必须与之对战，从而适应并改进其玩法。

为了有效地训练程序，它会与编码的对手在简单或困难模式下进行多次对战，模式在每局游戏开始时随机选择。这种在两种模式下训练的策略或机制，用于平衡探索和策略学习。在简单模式下，有空间探索棋盘状态和尝试不同的策略，阻力较小。在困难模式下，程序被置于一个必须深入思考并与更专业的对手对战的场景中。这为创造更复杂的战术奠定了基础。程序在每局游戏结束时更新其模型的权重。它会根据输赢逐渐学习和提高。这个迭代过程不仅会使程序在对抗不同对手和游戏情境时变得更强，还会把它变成一个更好的井字棋玩家。

训练程序

从本质上讲，训练程序意味着教会模型，即评估器，为对程序有利的棋盘状态给予高分，为不利的棋盘状态给予低分。程序将以自我对弈模式与一个编码的敌人对战。在学习开始时，评估器的权重被随机分配。这种随机性提供了一个基线，模型从零开始学习。它在一个名为“走法选择器”的函数中使用评估器来决定每局游戏的走法。程序和对手轮流走棋，直到游戏结束。这种重复的对弈创造了各种各样的情况，评估器需要学习如何评估。

游戏结束后，评估器进入训练阶段。最终棋盘状态的分数会根据游戏结果进行调整。如果程序获胜，则最终棋盘状态的分数为 1。如果输了，则分数为 -1。如果是平局，分数设置为 0。然后，这些分数被回溯，成为之前棋盘状态的分数。在这个回溯过程中，这一步的重要性不容忽视，因为它使评估器能够看到导致该结果的走法顺序，从而识别出导致胜利或失败的棋盘状态模式。

然后，使用修正后的分数和棋盘状态来更新评估器的权重。模型会优化权重，使评估器能更好地估计棋盘状态的评估值并预测结果。这个过程会重复数十万局游戏。通过这种方式，模型从大量不同的情况和策略中学习。模型将逐渐变得更擅长为预示胜利的棋盘状态返回更高的分数，为不太有希望的位置返回更低的分数。这种持续学习和调整的过程最终会提高程序的策略决策能力，并改善其整体游戏水平。

输出

现在我们将运行 200,000 局程序和对手之间的井字棋游戏。记录每局游戏的结果；绘制程序在固定游戏间隔内的胜/负/平分布图。

输出

评估

现在我们将绘制胜、平、负次数与游戏局数的关系图

输出

从上图中可以注意到，随着程序与对手进行的游戏越来越多，其胜率增加，败率减少。

除了这张图所呈现的内容，我无法做出任何更具体的观察，因为训练过程是嘈杂的，每次运行此内核时，上图都会有所不同。