人工智能中的 A* 搜索算法

A*（发音为“A-star”）是一种强大的人工智能和计算机科学中的图遍历和路径查找算法。它主要用于在图中找到两个节点之间的最短路径，同时考虑从当前节点到目标节点的估计成本。该算法的主要优势在于，与Dijkstra算法等传统搜索算法相比，它能够以更具信息量的方式探索图，从而提供最优路径。

A*算法结合了其他两种搜索算法的优点：Dijkstra算法和贪婪最佳优先搜索。与Dijkstra算法一样，A*确保找到的路径尽可能短，但通过类似贪婪最佳优先搜索的启发式函数来指导搜索，从而提高了效率。启发式函数，表示为h(n)，用于估计从任意给定节点n到目标节点的成本。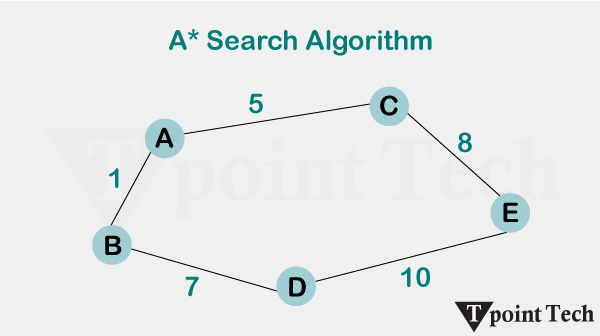

A*搜索算法的公式

正如我们所知，A*搜索算法用于识别图中从一个节点到另一个节点的最具成本效益和最短的路径。

让我们来看看我们用来找到从一个节点到另一个节点探索最短路径的总成本的公式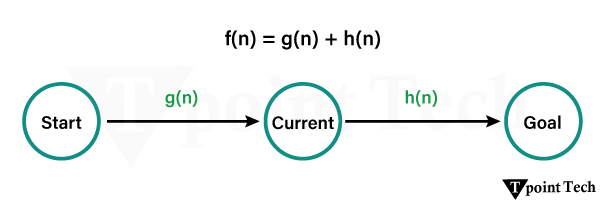

f(n)=g(n)+h(n)

其中，

• f(n): f(n)表示从起始节点经由当前节点n到达最终状态所产生的总成本。
• g(n): 从起始节点到节点n的实际成本。它代表节点n的出边成本之和。
• h(n): 从节点n到目标节点n的启发式成本（也称为“估计成本”）。这个特定于问题的启发式函数必须是可接受的，这意味着它从不过高估计达到目标的实际成本。节点n的评估函数定义为f(n) = g(n) h(n)。

A*算法根据f(n)的最低值来选择要探索的节点，优先选择到达目标估计总成本最低的节点。A*算法的工作原理

关键组成部分

让我们来理解A*搜索算法的关键组成部分

• 节点：节点是图中的点（连接相遇的地方）
• 边：节点之间的连接
• 路径成本：从一个节点到另一个节点的遍历成本。
• 启发式：从当前节点到最终或目标节点的估计遍历成本
• 搜索空间：所有可探索路径的集合

A*搜索算法如何工作？

A*搜索结合了Dijkstra算法和贪婪最佳优先搜索的原理。这使得A*搜索算法兼具两者的优点。

让我们快速回顾一下这两种算法的解释

• Dijkstra算法： Dijkstra算法有助于找到从给定源节点到图中所有其他节点的最短成本路径。
• 贪婪最佳优先搜索算法： 在贪婪最佳优先搜索算法中，选择估计离目标状态最近的节点进行扩展。

两种算法的优点相结合，形成了A*搜索，使其比单独使用时更有效、更准确。

A*算法的分步实现

• 初始化： 第一步，将初始节点放入优先级队列。优先级队列包含所有待评估的节点。它也称为开放列表。
• 评估： 第二步，从队列中选择f(n)值最低的节点进行下一个处理。
• 扩展： 在上一步评估中选择的f(n)值最低的节点与其邻居进行比较。
• 更新： 比较后，如果邻居节点的f(n)值低于先前记录的值，则进行更新并将其添加到开放列表中。
• 目标检查： 在此步骤中，进行目标检查以确定是否达到了目标节点。如果开放列表为空，也可以确认这一点，这表明没有更多可供进一步遍历的内容了。
• 重构： 最后一步，通过从最终或目标节点或初始节点回溯或跟踪步骤来重构路径。

A*搜索算法的伪代码

在查看A*搜索算法在Python中的实际实现之前，让我们先看看伪代码以了解其工作原理。

现在，我们准备查看A*搜索算法在Python中的实现。

在Python中实现A*搜索算法

让我们通过代码来看一下A*搜索算法在Python中的实现。

代码

输出

[(0, 1), (1, 1), (2, 2), (2, 3), (1, 4), (2, 5), (2, 6)]

说明

在上面的示例中，我们展示了一个使用迷宫表示法的A*搜索算法示例，它是一种欧几里得距离启发式函数。

在迷宫表示法中，0是可通行的，1是障碍物。允许8种移动方式，包括上、下、右、左和对角线。它使用heapq库作为开放列表来选择f(n)最低的列表，公式为f(n)= g(n) + h(n)。我们定义了起点和终点节点。

最后，它以坐标列表的形式返回最优且高效的路径。

理解启发式搜索h(n)

启发式函数h(n)在A*搜索算法中起着至关重要的作用，因为它有助于找到从当前节点到最终或目标节点的估计遍历成本。

有几种类型的启发式搜索。让我们详细了解一下

曼哈顿距离： 曼哈顿距离通过将当前位置和目标位置的x和y坐标之间的净差值相加来计算。

听起来很困惑，对吧？让我们用一个你在几何学中学过的公式来理解。

公式

h(n) = |x _当前 - x _目标| + |y _当前 - y _目标|

其中，

h(n) = 启发式函数

欧几里得函数： 欧几里得距离通过将当前位置和目标位置的x和y坐标之间的差值的平方和开平方来计算。

让我们把上面的陈述变成一个公式。

公式

h(n) = √(x _当前 - x _目标)² + (y _当前 - y _目标)²

对角线距离：当可能的方向移动数为8时，测量对角线距离。例如，扫地机器人或国际象棋中的王。

让我们把上面的陈述变成一个公式。

公式

h(n) = max(|x_当前 - x_目标|, |y_当前 - y_目标|

人工智能中A*搜索算法的优点

A*搜索算法在人工智能和问题解决场景中提供了多种优势

1. 最优解： A*保证在具有可接受启发式函数的加权图中，找到从起始节点到目标节点的最佳（最短）路径。这种最优性在许多需要找到最短路径的应用中具有决定性优势。
2. 完整性： 如果存在解决方案，A*会找到它，前提是图没有无限成本。这种完整性保证A*可以利用现有的解决方案。
3. 效率： 如果使用高效且可接受的启发式函数，A*则很高效。启发式函数通过关注有希望的路径并避免不必要的探索来指导搜索到目标，从而使A*比非感知搜索算法（如广度优先搜索或深度优先搜索）更有效。
4. 通用性： A*广泛应用于各种问题领域，包括寻路、路线规划、机器人技术、游戏开发等。只要能定义有意义的启发式函数，A*就可以高效地找到最优解。
5. 优化搜索： A*维护一个优先级顺序，以选择f(n)值（g(n)和h(n)之和）最低的节点进行扩展。这使其能够优先探索有希望的路径，从而减少搜索空间并加快收敛速度。
6. 内存效率： 与某些其他搜索算法（如广度优先搜索）不同，A*仅在优先级队列中存储有限数量的节点，这使其内存效率很高，尤其适用于大型图。
7. 可调启发式： A*的性能可以通过选择不同的启发式函数进行微调。更具教育意义的启发式函数可以更快地收敛并减少扩展的节点。
8. 广泛研究： A*是一个成熟的算法，拥有数十年的研究和实际应用。许多优化和变体已经被开发出来，使其成为一个可靠且易于理解的故障排除工具。
9. 网络搜索： A*可用于基于Web的路径搜索，算法根据环境变化或新元素的出现不断更新路径。它使得在动态场景中能够进行实时决策。

人工智能中A*搜索算法的缺点

尽管A*（字母A）搜索算法是解决AI路径查找和图遍历问题的广泛使用且强大的技术，但它也有缺点和局限性。以下是该搜索算法的一些主要缺点

1. 启发式准确性： A*算法的性能在很大程度上取决于用于估计从当前节点到目标的成本的启发式函数的准确性。如果启发式不可接受（从不过度估计实际成本）或不一致（满足三角不等式），A*可能找不到最优路径，或者可能探索比必要更多的节点，从而影响其效率和准确性。
2. 内存使用： A*要求所有已访问的节点都保存在内存中，以便跟踪已探索的路径。当处理大型搜索空间或有限内存资源时，内存使用有时会成为一个重要问题。
3. 时间复杂度： 尽管A*通常很高效，但对于巨大的搜索空间或图，其时间复杂度可能令人担忧。在最坏的情况下，如果启发式不适用于问题，A*找到最优路径可能需要指数级的时间。
4. 目标节点瓶颈： 在某些特定场景下，A*算法在最终到达目标区域之前需要探索离目标很远的节点。当启发式需要有效地将搜索引导到目标时，就会出现这个问题。
5. 成本绑定： 当多个节点具有相同的f值（实际成本与启发式成本之和）时，A*会遇到困难。所使用的策略会影响发现路径的最优性和效率。如果处理不当，可能导致不必要的节点被探索并减慢算法速度。
6. 动态环境中的复杂性： 在边缘或节点成本在搜索过程中可能发生变化的动态环境中，A*可能不适用，因为它不能很好地适应此类变化。从头开始的重新制定可能计算成本很高，而D*（动态A*）算法被设计用来解决这个问题。
7. 无限空间中的完美性： A*在无限状态空间中可能找不到解决方案。在这种情况下，它可能会无限运行，探索越来越多的节点而找不到解决方案。尽管存在这些缺点，A*仍然是一个健壮且广泛使用的算法，因为它在许多实际情况下可以有效地找到最优路径，前提是启发式函数设计良好且搜索空间可管理。已经提出了A*的各种变体和变种来缓解其一些局限性。

人工智能中A*搜索算法的应用

A*（字母A）搜索算法是一种在人工智能和计算机科学中广泛使用且健壮的路径查找算法。其效率和最优性使其适用于各种应用。以下是A*搜索算法在人工智能中的一些典型应用

1. 游戏寻路： A*常用于电子游戏中，用于角色移动、敌人AI导航以及在游戏地图上查找从一个位置到另一个位置的最短路径。它能够根据成本和启发式找到最优路径，非常适合游戏等实时应用。
2. 机器人和自动驾驶汽车： A*用于机器人和自动驾驶汽车导航，以规划机器人到达目的地的最优路线，避开障碍物并考虑地形成本。这对于在自然环境中高效安全地移动至关重要。
3. 迷宫求解： A*可以有效地找到迷宫中的最短路径，使其在许多迷宫求解应用中具有价值，例如解决谜题或导航复杂结构。
4. 路线规划和导航： 在GPS系统和地图应用中，A*可以用于在地图上查找两点之间的最优路线，同时考虑距离、交通状况和道路网络拓扑等因素。
5. 益智游戏： A*可以解决各种图画谜题，如滑块拼图、数独和8拼图问题。资源分配：在需要最优分配资源的场景中，A*可以帮助找到最有效的分配路径，从而最大限度地降低成本并提高效率。
6. 网络路由： A*可用于计算机网络，以找到数据包从源节点到目标节点的最有效路径。
7. 自然语言处理（NLP）： 在某些NLP任务中，A*可以通过搜索可能性词序列来生成连贯且相关的响应，这些响应基于它们的可能性和相关性。
8. 机器人路径规划： A*可用于规划机器人从一个点到另一个点的路径，同时考虑各种约束，例如避开障碍物或最大限度地减少能耗。
9. 游戏AI： A*也用于为非玩家角色（NPC）做出智能决策，例如确定到达目标的最佳方式或在团队游戏中协调移动。

A*搜索算法与其他搜索算法的比较

结论

作为人工智能领域强大且通用的工具，A*搜索算法因其在路径查找和图遍历问题中的卓越效率而享有盛誉。A*智能地将g(n)的实际成本与到目标的估计成本h(n)相结合，并以最优的方式进行探索，同时在某些条件下仍然是完整的。

它充当了广度优先搜索或Dijkstra算法等完全穷举搜索策略与启发式开发技术（如贪婪最佳优先搜索）之间的桥梁。这种平衡结构使得A*能够在低探索率下实现最优性。

常见问题解答 (FAQs)

1. 什么是A*搜索算法？

A*搜索算法用于识别图中从一个节点到另一个节点的最具成本效益和最短的遍历路径。

这是我们使用的公式

f(n)=g(n)+h(n)

2. A*中的g(n)是什么？

g(n)表示从最后一个节点到达起始节点所需的成本。它等于节点n转移到其他节点的所有成本。

3. A*中的h(n)是什么？

启发式成本表示从给定节点n移动到目标节点所需的估计距离或努力。可接受的启发式函数是指从不低估达到目标的实际成本的函数。

4. A*中常用的启发式函数有哪些？

A*中最常用的启发式函数是

• 曼哈顿距离 - 曼哈顿距离通过将当前位置和目标位置的x和y坐标之间的净差值相加来计算。
• 欧几里得距离 - 欧几里得距离通过将当前位置和目标位置的x和y坐标之间的差值的平方和开平方来计算。
• 对角线距离 - 当可能的方向移动数为8时，测量对角线距离。例如，扫地机器人或国际象棋中的王。

5. A*在现实生活中用在哪里？

A*搜索算法用于以下领域

• GPS和地图（Google地图）
• 机器人导航
• 电子游戏中的AI
• 益智游戏（例如，8拼图，鲁比克方块）
• 网络路由