MATLAB 中的协方差

引言

掌握数据集中变量之间的关系需要掌握 MATLAB 中的协方差。两个随机变量一起变化的量由协方差衡量。正协方差表示变量之间的正相关关系，而负协方差表示反相关关系。当协方差值为零时，变量之间没有线性关系。

MATLAB 提供了 cov 和 corr 等多种函数来计算协方差。在计算数据集的协方差矩阵时，cov 函数非常有用。

以下是使用 MATLAB 的 cov 函数的快速概述

语法

X：输入数据，其中一列代表一个变量，一行代表一个观测值。

C：协方差矩阵。如果 X 有 n 列，则矩阵 C 是 n x n 的对称矩阵。变量在列 i 和列 j 之间的协方差由元素 C(i,j) 表示。

理解协方差矩阵

通过 cov 函数生成的协方差矩阵可以深入了解数据集中变量之间的关系。协方差矩阵的每个元素都表示两个不同变量之间的协方差。零值表示线性关系，负值表示负关系，正值表示正关系。

• 通过识别倾向于一起变化的变量以及独立的变量，对协方差矩阵的分析可以揭示数据集的结构。
• 此外，协方差值的大小表明了变量之间相关性的强度。

分析结果

理解数据集中的基本模式和关系需要对协方差矩阵进行解释。在解释过程中，以下是一些需要记住的重要事项：

正协方差：当两个变量具有正协方差时，它们通常会一起增长或一起下降。这表明变量之间存在正相关关系，并且平均而言，当一个变量上升时，另一个变量也倾向于随之上涨。

负协方差：另一方面，负协方差表示变量之间存在反比关系。当一个变量增长时，另一个变量倾向于下降，反之亦然。

零协方差：当变量之间没有线性关系时，假设它们是独立的。重要的是要记住，即使两个变量的协方差为零，它们可能仍然以非线性方式相关。

如何计算相关系数

尽管协方差矩阵提供了有价值的信息，但它需要标准化，这使得跨数据集的比较变得困难。MATLAB 中的 corr 函数计算相关矩阵以解决此问题。相关矩阵包含相关系数，这些相关系数是变量之间关联的标准化估计值，范围从 -1 到 1。

语法

X：数据矩阵输入。每一列代表一个变量，每一行代表一个观测值。

R：相关矩阵。如果 X 有 n 列，则矩阵 R 是 n x n 的对称矩阵。矩阵 X 的列 i 和列 j 之间的相关系数由元素 R(i,j) 表示。

使用 corr 函数可以更有效地理解变量之间线性相关性的方向和强度。

示例

输出

首先，在此应用程序中创建了一个名为 X 的样本数据集，其中包含三个变量和五个观测值。接下来，我们使用 cov 函数计算数据集的协方差矩阵 C。最后，我们在 MATLAB 命令窗口中显示计算出的协方差矩阵 C 和数据集 X。

MATLAB 中的协方差应用

在统计学、金融学、经济学和数据科学等多个领域，了解 MATLAB 中的协方差至关重要。MATLAB 中协方差的关键应用包括以下几点：

投资组合分析：协方差对于投资组合分析至关重要，以理解不同资产之间的关系。它有助于评估不同资产之间分散投资的好处，并优化投资组合的整体风险和回报。

模式识别：在图像和信号处理等模式识别工作中，协方差分析至关重要。通过检查各种特征之间的协方差，可以找到数据中的重要模式和结构。

统计建模：协方差是统计建模的关键组成部分，它评估各种变量之间的相关性，并根据观测数据中的模式创建预测模型。

数据预处理：协方差分析有助于特征选择和降维等数据预处理任务。它有助于识别高度相关或重复的特征，可以删除这些特征以简化数据集。

最佳实践和注意事项

为了在 MATLAB 中处理协方差时确保准确和有意义的结果，考虑一些推荐的实践和安全措施至关重要。

数据预处理：在计算协方差之前，清理和预处理数据以消除可能扭曲结果的任何异常值或不一致之处。

归一化：如果需要，对数据进行归一化以确保变量在同一尺度上。尺度的差异可能会影响协方差结果。

解释注意事项：由于协方差仅表示变量之间的线性相关性，因此在解释其结果时应小心。协方差矩阵可能不足以表达非线性交互。

数据可视化：为了更好地理解变量之间的交互作用，可以使用热力图或其他可视化方法来可视化协方差矩阵和相关矩阵。

协方差是理解数据集中变量之间关系的基本统计量。

• 在 MATLAB 中，可以使用 cov 函数轻松计算协方差矩阵，可以使用 corr 函数计算相关矩阵，并获得标准化的关系度量。
• 通过利用这些功能并理解协方差分析的含义，用户可以做出明智的决策，从他们的数据中获得深刻的见解，并为各种应用创建强大的统计模型。
• MATLAB 强大的计算能力使其成为一项必不可少的工具，用于

示例

输出

说明

示例数据集

X 的示例数据集由该矩阵表示，其中每列代表一个变量，每行代表一个观测值。

协方差矩阵

协方差矩阵显示了数据集中变量之间的相关性。列 i 和列 j 之间的协方差由矩阵 CovMatrix(i, j) 的每个元素表示。

相关矩阵

相关矩阵显示了数据集中变量之间的相关系数。列 i 和列 j 之间的相关性由矩阵 CorrMatrix(i, j) 的每个元素表示。

• 这些矩阵揭示了变量之间的关系，其中相关矩阵显示了标准化的相关性，而协方差矩阵显示了原始关系。
• 在矩阵中，接近零的值表示弱或不存在的关系；正值表示正关系，负值表示负关系。

将协方差矩阵可视化为热力图

示例

输出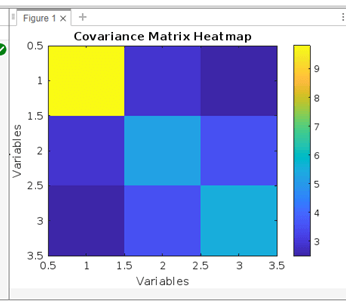

说明

该应用程序将协方差矩阵 C 可视化为热力图。热力图中显示了数据集 X 中变量各种对之间的协方差值。较冷的色调表示负协方差，而较暖的色调表示更强的正协方差。通过 colorbar 函数提供的颜色刻度可以轻松理解协方差值的大小。

• 绘图类型由标题“协方差矩阵热力图”指示； xlabel 和 ylabel 函数提供了更多可视化上下文，它们分别标记了轴上的变量。
• 用户可以通过使用此可视化轻松发现数据集中变量之间的模式和关系，这提供了一种评估协方差矩阵的便捷方法。

示例

数据预处理和协方差计算

输出

该软件在计算预处理数据的协方差矩阵之前，创建、居中并向随机数据集添加噪声。居中数据显示在预处理数据集 X_centered 中，预处理数据集中变量之间的协方差显示在协方差矩阵 C 中。