MATLAB limit

引言

在数学分析中，函数在变量趋近于特定值时如何表现是一个基本概念。理解这种行为，尤其是在微积分和数学分析的背景下，在很大程度上取决于极限的概念。极限函数是著名的计算机程序 MATLAB 提供的一个关键工具，它允许用户以符号方式确定函数极限。

理解极限的概念

当理解函数在特定点附近或变量趋近于特定值时的行为时，极限至关重要。它们在许多数学领域都很重要，包括微积分、微分方程和实分析，它们有助于确定函数在关键点附近的行为。通过评估极限，数学家和科学家可以更多地了解函数在各种情况下的行为，为进一步的数学研究和问题解决奠定了坚实的基础。

极限在 MATLAB 操作中的重要性

• MATLAB 中的极限函数是一个强大的计算工具，可以简化符号计算极限。MATLAB 允许用户通过利用符号数学工具箱的符号处理数学表达式的能力来评估复杂的极限、导数、积分和其他数学运算。
• 该函数在学术和实际环境中都非常宝贵，使研究人员、工程师和学生能够有效地进行复杂的分析并探索复杂的数学主题。

语法

MATLAB 中极限函数的语法如下

参数如下

f：需要计算极限的表达式或函数。

x：计算极限所针对的变量。

a：变量 x 趋近的值。

输出 L 表示 f 的极限，当 x 趋近于值 a 时。

MATLAB 的符号数学工具箱包含极限函数

在微积分和数学分析中，极限的概念至关重要，因为它阐明了函数在特定点附近或变量趋近于特定值时的行为。

MATLAB 的符号数学工具箱包含极限函数，它使用户能够以符号方式处理和操作数学语句，而不是以数量方式。MATLAB 允许用户通过利用符号计算来执行复杂的数学运算，例如极限、导数、积分等的评估。

示例

输出

此代码示例中的 `syms x` 命令使得可以将变量 x 视为符号变量，从而可以使用符号表达式和运算。微积分极限评估有时会用函数 f 来说明，该函数定义为 x 的正弦除以 x。接下来，当 x 趋近于零时，极限函数确定函数的极限。然后，`disp` 函数显示计算出的极限。

• 要使用 MATLAB 中的符号表达式和计算，必须拥有符号数学工具箱。它提供了许多用于符号数学的工具和函数，使用户能够执行许多手动执行起来困难或耗时的数学运算和分析。

符号向量表达式的极限

使用符号数学工具箱中的极限函数，您可以使用 MATLAB 查找符号向量中表达式的极限。在处理涉及符号向量的表达式时，您必须考虑用于计算极限的向量的特定分量。只要您指示沿向量元素的极限方向，极限函数就可以处理这些情况。

示例

输出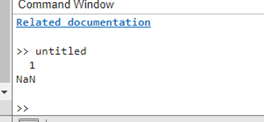

说明

此行声明符号变量 x 和 y。

f1 = sin(x)/x; - 变量 f1 表示符号向量表达式的第一个元素，即 sin(x)/x。

f2 = cos(y)/y; - 符号向量表达式的第二个分量 cos(y)/y 由变量 f2 表示。

L1 = limit(f1, x, 0); - 当 x 趋近于 0 时，此行计算第一个元素 f1 的极限。

L2 = limit(f2, y, 0); - 当 y 趋近于 0 时，此行计算第二个元素 f2 的极限。

L = [L1; L2]; - 在这种情况下，我们构建最终向量 L，其中包含每个元素计算出的极限。

Disp (L); - 此行显示计算出的极限组成的向量。