MATLAB 中的阶乘函数

引言

通过数学运算阶乘的数字分解产生结果集，方法是将 1 到指定数字之间的每个整数值相乘。运算符用 n! 表示非负整数 n 的阶乘，其定义如下：

n! = n × (n - 1) × (n - 2) × … × 1

阶乘运算因其基本性质以及解决组合和概率问题的能力，在数学、计算机科学和应用科学中得到广泛应用。

• 定义 0! = 1（通过基本定义，因为数学运算需要 1 才能保持一致）。
• 阶乘仅存在于非负整数。

阶乘的数学表示 (n!)

阶乘可以数学表示为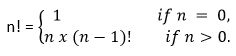

通过这个阶乘定义，编程递归变得清晰，它依赖于之前的阶乘运算。

例如

• 5! = 5 × 4 × 3 × 2 × 1 = 120
• 3! = 3 × 2 × 1 = 6

随着 n 的增加，即使 n 保持中等屏幕状态，阶乘也会产生大量的数值。

阶乘的实际应用

许多实际场景以及多个数学领域都严重依赖阶乘来达到其目标。

1. 组合学： 需要排列和组合解决方法的问题广泛使用阶乘。
   • 排列： 排列 n 个不同项目的方法数由 n! 给出。
     示例：将 4 个项目并排放置会生成 4! = 24 种不同的序列选项。
   • 组合： 要从 n 个项目中选择 r 个项目而忽略排列顺序，我们使用公式
     
2. 概率论
   阶乘在计算各种场景中的概率时至关重要，例如
   • 二项式概率分布： 该工具帮助确定顺序试验的概率结果。
   • 泊松分布： 在罕见事件的情况下，阶乘出现在分母中以建立数学模型。
3. 数学级数和展开
   阶乘出现在级数展开中，例如
   • 泰勒级数和麦克劳林级数： 阶乘中的分母有助于计算处理函数 ex、sin(x) 和 cos(x) 时出现的展开项。
   • 示例：e^x 的泰勒级数展开为
     e^x = ∑xⁿ/n!
4. 计算机科学和算法
   算法开发人员利用阶乘来创建递归解决方案和动态规划技术，这些技术与分治法相结合，解决了复杂的计算难题。在世界范围内的多个学科中，阶乘作为数学上的奇特现象而存在，同时具有许多实际和理论应用。

MATLAB 中的阶乘函数

在 MATLAB 中，阶乘函数作为一个集成功能，可以自动计算阶乘数，无论是独立计算还是通过数组计算。该工具以简单的处理选项和灵活的数据输入要求提供快速性能，以满足多个数学、统计和工程需求。

MATLAB 的阶乘函数用户可以通过将从 1 到 n 的正整数相乘来确定任何指定数字 n! 的阶乘值。

例如：n! = n × (n - 1) × (n - 2) × ⋯ × 1，其中 0! = 1

鉴于当 n 值增加时阶乘的快速扩展，MATLAB 提供了其专门的阶乘计算工具，以实现高效的阶乘计算性能。

阶乘函数的主要特点包括：

• 系统接受标量和数组值输入。
• 处理工具实现自动数字类型管理，在处理大数值时保持精度。
• 基本语法提供了降低编程复杂性的替代方法。

语法

使用阶乘函数的语法很简单：

• n： 软件需要一个输入值，该值需要计算其阶乘值。输入可以是标量或数组条件。
• F： 计算出的阶乘值。MATLAB 根据输入返回不同的结果，输入可以是单个值或多个数据点。

输入和输出

1. 有效输入类型
   阶乘函数支持以下输入类型：
   • 标量输入： 单个非负整数（例如，factorial(5) 返回 120）。
   • 数组输入： 非负整数数组（例如，factorial([3, 4, 5]) 返回 [6, 24, 120]）。
   • 输入必须是整数。阶乘函数只接受正整数输入。所有其他值都会导致错误输出。
2. 输出解释
   • 当给定标量输入数据时，单个数值输出显示输入值的阶乘计算。
   • 输入数组时，阶乘的单元通过计算每个输入元素的阶乘值来操作，从而产生一个数组输出，其中每个元素都等于其相应输入值的阶乘。
   • MATLAB 的浮点精度定义了一个最大值限制，可以处理高达 170 的精确结果。当结果值超出允许范围时，存在数值精度截止。

示例

1. 标量输入

2. 数组输入

3. 处理边缘情况

• 0 的阶乘

• 大输入值

通过 MATLAB 中的阶乘函数，用户可以获得对单个整数和数组的阶乘值计算的基本处理能力。其决定性和直接操作使其成为众多主题中数学生成的主要选择。

MATLAB 中阶乘函数的使用示例

1. 基本示例：计算单个整数的阶乘

通过 MATLAB 中的阶乘函数，用户可以轻松确定单个整数的阶乘计算。例如：

输出

 
Factorial of 5 is: 120   

在这里，函数计算 5! = 5 × 4 × 3 × 2 × 1 = 120，演示了阶乘函数对单个整数输入的直接使用。

2. 数组输入示例：数字数组的阶乘

MATLAB 的阶乘处理功能通过元素特定的阶乘计算对整数数据数组进行操作。

输出

 
Factorials of the array elements:
     6    24   120   

在此示例中

• 3!=6
• 4!=24
• 5!=120

凭借其功能，该函数对完整的数组输入执行阶乘计算。

3. 边缘情况：0 和大数的阶乘

阶乘函数通过始终对 00 阶乘返回 11 来解决两种情况，同时在处理大数时管理扩展精度。

0 的阶乘

输出

 
Factorial of 0 is: 1   

大数的阶乘： MATLAB 使用双精度提供大数的阶乘结果。非常大的阶乘计算可能会超出标准精度能力，因此它们只提供近似解值。

输出

 
Factorial of 170 is: 7.257415615308004e+306   

对于 n > 170，由于超出双精度限制，结果返回为 Inf。

MATLAB 中阶乘增长的可视化

阶乘的指数增长

输入值的增长与阶乘呈指数关系。这些快速的阶乘大小结果对组合学具有实用价值，同时在计算机性能和图形表示方面造成了复杂性。例如：

• n! = n × (n - 1) × (n - 2) × … × 1
• 对于 n = 5，5! = 120；对于 n = 10，10! = 3,628,800。

可视化显示阶乘的增长速度超过了线性或多项式函数的速度。

绘制一系列值的阶乘

在 MATLAB 中可视化阶乘增长：

1. 定义范围： 要计算阶乘，请在整数范围内选择几个数字，包括 1 到 20 作为测试值。
2. 计算阶乘： 使用 MATLAB 的内置阶乘函数。
3. 绘制结果： 详细的视觉显示需要实施绘图以显示获得的结果。

以下是绘制阶乘增长的 MATLAB 代码：

结果分析与解释

• 指数增长： 该图显示了 n 值大于或等于 10 时，值呈近乎垂直的上升趋势，指出阶乘增长中的指数模式。
• 数据表示的限制： 高 n 值的阶乘超出了传统数值精度，因此它们需要对数缩放或近似分析方法。
• 实用洞察： 阶乘增长模式的分析有助于识别可以处理频繁阶乘的任务，并结合战略决策来选择替代计算技术，例如斯特林近似或对数阶乘。
• 阶乘增长超过指数函数和多项式函数，造成影响分析和计算的可视化问题。

阶乘在 MATLAB 中的应用

1. 组合学：计算排列和组合

在组合学中，阶乘是计算排列顺序选择问题中可能性的基本数值工具。通过其阶乘函数，MATLAB 提供了直观的功能，可以轻松生成数据排列或组合。

• 排列： 排列是指项目排列，其中顺序很重要。排列的公式为：

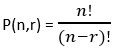在 MATLAB 中，您可以使用阶乘函数计算排列：

• 组合： 没有顺序优先级的项目选择定义了组合。组合的公式为：

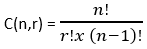组合的 MATLAB 代码：

2. 级数展开：泰勒级数和二项式定理中的阶乘

计算块严重依赖阶乘，因此它们可以执行泰勒级数和二项式定理。

• 泰勒级数： 函数 f(x) 在 x=0 附近的泰勒级数展开为：

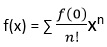在 MATLAB 中使用泰勒级数近似 exe^x 的示例：

• 二项式定理： 二项式定理表示 (a+b)ⁿ 的展开式为：

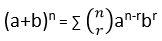MATLAB 示例：

3. 概率：概率分布中的阶乘

阶乘在泊松分布和其他概率分布中保持核心重要性，因为它们决定了事件在预定时间间隔内发生的可能性。

• 泊松分布： 概率质量函数为：
  P(X=k) = λ^ke^−λ/k!

在 MATLAB 中计算泊松概率的示例：