MATLAB Trapz

MATLAB 函数 trapz (x, y, n)，其中 y 是 x 的积分，使用梯形规则逼近函数 y=f(x) 的积分，而 n（可选）沿维度 n 执行积分。

语法

示例 1

使用 MATLAB 函数 trapz (x, y) 逼近积分的成本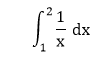

并与精确值进行比较，评估当 n=5 和 n=10 时的百分比误差。

解决方案

精确值从以下公式求得：

对于使用梯形规则的近似，我们设 x₅ 代表 n=5 的行向量，x₁₀ 代表 n=10 的向量，即 ∆x =1/5 和 ∆x=1/10。 相应的值表示为 y₅ 和 y₁₀，曲线下的面积分别表示为 area5 和 area10。

创建以下脚本

MATLAB 显示以下结果

当使用 ∆x =1/5 时，百分比误差为

当使用 ∆x =1/10 时，百分比误差为

示例 2

积分

其中 τ 是积分的虚拟变量，称为误差函数，它广泛应用于通信理论中。 使用 MATLAB trapz (x, y) 函数找到此积分下 n=10 且积分上限为 t=2 时的面积。

解决方案

创建以下脚本

MATLAB 显示以下结果

Example3

非线性电机的 i-v（电流-电压）关系由下式给出

其中 v(t)=sin3t。

通过任何方式，求

• 瞬时功率为
  p(t)=v(t)i(t)=0.1 sin3t(e^0.2sin3t-1)
• 能量是瞬时的积分是
  

可以使用分部积分法分析求解最后一个积分，但这并不容易。 我们可以尝试使用 MATLAB int (f, a, b) 函数，其中 f 是一个符号表达式，a 和 b 分别是积分的下限和上限。

当 MATLAB 无法找到解决方案时，它会返回警告。 例如，当尝试使用方程式的符号表达式进行积分时，MATLAB 返回以下消息

当执行此脚本时，MATLAB 显示以下消息。

接下来，我们将使用 MATLAB trapz (x, y) 函数通过梯形规则找到并绘制功率和能量。 对于此示例，我们选择 n=100，因此 ∆x=1/100。 下面的 MATLAB 脚本将计算并绘制功率。

如图所示，功率以均匀的方式变化

下面的 MATLAB 脚本计算并绘制能量。

因此，能量值为 0.1013 焦耳。 能量如图所示