MATLAB 辛普森法则

梯形法则和辛普森法则是牛顿-科茨公式的特殊情况，该公式使用更高阶函数进行数值积分。

设抛物线代表图形的曲线。

y=αx²+βx+γ…………..方程 1

该方法在区间 -h≤x≤h 下的面积为

曲线通过三个点(-h,y₀ ),(0,y₁ ),和 (h,y₂ )。 那么，通过一个方程，我们有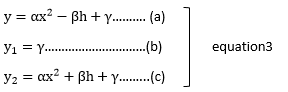

我们现在可以评估系数 α,β,γ 并用 h, y₀, y₁ 和 y₂ 表示方程 2。

通过将方程 3 的 (b) 代入 (a) 和 (c) 并重新排列，我们得到

αx²-βh=y₀-y₁…..方程 4

αx²+βh=y₂-y₁…..方程 5

将方程 4 与方程 5 相加得到

2αh²=y₀-2y₁+y₂…...方程 6

并通过代入方程 2，我们得到

现在，我们可以将方程 8 应用于区间 a≤x≤b 中任意曲线 y=f(x) 的连续段，如图所示。

我们观察到，抛物线可以通过其端点和中点来近似曲线的每个宽度为 2h 的段。 因此，AB 段下的面积为

同样，BC 段下的面积为

等等。 当每个段下的面积相加时，我们得到

由于每个段的宽度为 2h，要应用辛普森数值积分法则，细分的数量 n 必须为偶数。 此限制不适用于梯形数值积分法则。

方程 11 的 值为从