MATLAB 中的矩阵与数组

• MATLAB 一次性处理整个矩阵和数组。
• 所有类型的数据变量都存储为多维数组，无论是字符、字符串还是数字。
• 二维数组称为矩阵，常用于线性代数。

MATLAB 中的数组创建

我们可以在 MATLAB 中通过多种方式创建数组

• 通过在元素之间留空格

• 此命令创建一个名为“A”的数组变量，该变量具有一行四列。
• “A”变量存储在工作区中，输出将在命令窗口中显示为

• 通过在元素之间使用逗号

• 此命令将创建一个名为“a”的数组变量，该变量具有一行四列。
• “a”变量存储在工作区中，输出将在命令窗口中显示为

• 我们可以将这两种方法结合起来，但这并非良好的实践。

它的作用与之前相同，但为了更好的语法，请避免使用。

• 元素在单行中的数组称为行向量。或者我们可以说一维数组是向量。
• 二维数组称为矩阵。这意味着矩阵有多个行和列。因此，在创建具有多行的矩阵时，我们必须用分号分隔行。

• 创建矩阵时要小心，每行应具有相同数量的列，并且每行应以分号分隔。否则，将会显示错误并且不会创建矩阵。

• 我们可以使用内置函数创建矩阵，例如 ones、zeros 或 rand。

MATLAB 中的矩阵和数组运算

MATLAB 支持两种类别的数组运算，称为**数组运算**和**矩阵运算**。

数组运算是**逐元素**在数组之间实现的运算。也就是说，该运算在两个数组的对应元素上实现。

例如：

注意： 两个数组的行数和列数必须相同。否则，MATLAB 将生成错误消息。

下表提供了 MATLAB 中两个标量之间算术运算的摘要。

两个标量之间的算术运算

操作	代数形式	MATLAB 形式
加法	a + b	a + b
减法	a - b	a - b
乘法	a x b	a * b
除法		a / b
幂运算		a ^ b

数组运算也可以出现在数组和标量之间。如果运算在数组和标量之间进行，则标量的值将应用于数组的每个元素。

例如：

矩阵运算

矩阵运算遵循线性代数的标准规则，例如矩阵乘法。在线性代数中，乘积 c=a x b 由以下等式定义。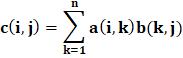

例如：

注意： 矩阵 a 的列数必须等于矩阵 b 的行数。

MATLAB 使用特殊符号来区分数组运算和矩阵运算。在数组运算和矩阵运算具有不同定义的场景中，MATLAB 使用句点放在符号前以表示数组运算（例如，.*）。

下表列出了标准的数组和矩阵运算。

矩阵和数组运算示例

• 我们可以使用单个算术运算符来处理矩阵中的所有值。

• 这里需要注意的一点是，当我们输入命令 a + 5 时，它不会改变原始变量“a”，直到我们再次将其赋值为输出。
• 这就是为什么上面的输出被赋值给默认变量“ans”。
• 我们也可以使用单个函数来处理整个矩阵。

• 我们可以通过在注释行前使用 '%' 百分号来输入注释。
• 在变量后使用单引号 (') 来转置矩阵。

• 矩阵的转置将每一行变成一列。
• 在 MATLAB 中，除了矩阵乘法，我们还可以执行逐元素乘法。
  让我们通过一个例子来理解逐元素乘法和矩阵乘法的区别

MATLAB 中的 Format 命令

MATLAB 在内部将所有数字存储为浮点值，最多可达 15 位小数。但它通常显示最多 4 位小数。让我们看一个例子。

• 现在我们将使用 format 命令显示 MATLAB 中最大可能小数点的结果

• Format 命令语法：在命令提示符处输入“format long”。
• 此格式将一直有效，直到我们更改 format 命令。
• 现在我们将使用另一个 format 命令来更改格式

MATLAB 中数组的连接

正如我们连接或连接字符串一样，在 MATLAB 中，我们也可以连接数组。在数组声明中使用的方括号 [ ] 本身就是连接运算符。

我们可以通过两种方式连接数组

• 水平连接
• 垂直连接

MATLAB 中的数组水平连接

• 规则：所有数组应具有相同的行数。
• 语法：将所有数组用方括号括起来，用逗号分隔，[a, b, c]。
• 示例

MATLAB 中的数组垂直连接

• 规则：所有数组应具有相同的列数。
• 语法：将所有数组用方括号括起来，用分号分隔，[a;b;c]。
• 示例

MATLAB 中复数的表示

• 复数既有实部也有虚部。
• 虚数单位的值等于 -1 的平方根。
  sqrt (-1) => 0.0000 + 1.0000i
• 使用字母“i”或“j”来表示复数的虚部。
• 示例

MATLAB 中的数组索引

在 MATLAB 中，每个变量都是一个数组。数组中的所有元素都按行和列进行索引。可以使用 MATLAB 中的索引来访问任何特定元素。MATLAB 中数组的索引与数学中的索引相同。它具有访问元素的其他语法。

MATLAB 中有几种索引元素的方法。

1. 通过指定行和列下标

• 引用数组特定分量的最常见方法是在方括号中指定行和列下标以及数组变量。
• 在指定的行和列的交叉点处搜索元素作为下标。

2. MATLAB 中的线性索引

• 使用单个下标代替行和列下标称为 MATLAB 中的线性索引。
• 通过按列向下遍历来搜索元素。

3. 引用 MATLAB 中数组的多个元素

• MATLAB 中有一个冒号运算符（:），用它来引用数组的多个元素。
• 示例

使用冒号运算符创建向量

通过使用冒号运算符，我们可以创建等间隔值向量。我们可以分配步长值，该值可以以固定间隔影响下一个值。

• 语法： start: step: end。
• 示例
  让我们用冒号运算符来创建一个 13 的表格。

访问当前维度之外的数组元素

• 我们只能访问当前维度内的元素。这意味着如果它是一个向量并且包含九个元素，那么我们就不能访问第 12 个位置的元素。因为在向量创建期间没有定义第 12 个位置。
• 如果我们输入一个访问其当前维度之外的元素的命令，它将抛出错误，提示索引超出数组边界。

• 但是，我们可以为当前不存在的位置赋值。
• 例如，我们有一个包含 9 个元素的向量；然后，我们可以通过赋值来创建第 12 个元素或第 9 个元素之后的任何元素。

• 如果最后一个索引和新创建的索引之间存在任何间隙，则间隙索引将自动赋 0 值。
• 可以为所有数组中的索引赋一个值。