MATLAB 中的求和

引言

求和是 MATLAB（一种流行的技术和数值计算编程语言）完全支持的众多数学运算之一。计算一组数字的总体和以及序列中值的累积称为求和，它是一个基本的数学过程。MATLAB 提供了各种内置函数和工具，可以对数组、级数甚至连续函数进行求和。

• 我们将涵盖求级数、获取定积分、计算累积和以及对数组求和的基础知识。我们还将讨论如何使用求和函数中的可选参数来微调计算控制。

求和符号

求和符号是一种简洁有效的数学表示方法，用于表示一系列数字的总和。它通常用符号 ∑（大写希腊字母 sigma）表示。在科学、工程和数学中，它经常被用来简洁地解释重复的加法过程。该符号由几个基本元素组成，每个元素都对于指定求和的参数至关重要。

求和符号 (∑)：求和符号的核心符号 ∑，类似于大写的希腊字母 sigma。它表示需要将序列的元素相加。与 ∑ 符号右侧要相加的元素一起，陈述了求和变量的要求。

求和变量，或索引 (i)：求和变量，通常写成 "i"、"j" 或 "k"，表示进行求和的变量。索引显示在 ∑ 符号下方。它充当后续元素值的占位符。求和的下限和上限定义了索引的范围。

求和的下限（起始点）：这是索引的起始值，或求和开始的点。它表示求和开始的索引值。

求和的上限（停止点）：这是索引可以达到的最大值，表示求和的结束。

对从下限到上限（含）的每个索引值执行求和。

• 这些元素组合在一起，形成了求和符号中的一个表达式，该表达式简洁地表示了给定范围内一系列项的总和。
• 该符号可以表示许多数学运算，例如算术级数和几何级数的求和、级数以及其他数学函数。

例如，求和符号可用于表示前 n 个自然整数的和，如下所示：

其中 'i' 作为索引变量，表示从 1 到 n（含）的所有整数的总和。

同样，我们可以表示前 n 个自然整数的平方和如下：

在这种情况下，该符号表示从 1 到 n 的数字的平方和，其中 'i' 是索引变量，其值在 1 到 n 之间。

• 掌握求和符号的元素对于有效表示和理解数学运算和级数至关重要。
• 它为复杂的数学关系和概念提供了一种简洁而统一的表示方法，有助于在各种科学和学术领域中实现更易于理解的沟通和分析。

符号求和

在 MATLAB 中，`symsum` 函数是符号化求和的有效工具。因为它允许用户对符号表达式进行求和，所以在处理复杂的数学序列和级数时特别有用。

• 该函数根据提供的符号变量计算指定范围内表达式的总和。
• 该系统函数通常用于数学计算、物理、工程和其他需要符号操作的科学应用中。

S = symsum(s, i, a, b)

以下是对系统函数每个部分的详细解释：

S：这是符号输出，即符号求和的结果。它表示给定表达式在指定范围内的符号和。

s：这是需要求和的符号表达式或函数。它可以是简单的表达式，也可以是包含符号变量的更复杂的数学运算。

i：这代表求和索引或符号变量。它是随着和在其范围内移动而变化的变量。

a 和 b：它们分别代表求和的下限和上限。在求和过程中，它们指定了符号变量将变化的范围。

在评估各种数学级数（如算术级数、几何级数以及更复杂的无穷级数）时，`symsum` 函数非常有用。它使用户能够确定许多手工计算困难的求和的封闭形式解。通过利用 MATLAB 的符号数学功能，此函数提供了一种在 MATLAB 环境中管理符号表达式和计算的实用方法。

数组求和

在 MATLAB 中查找数组元素的总和是一个简单但重要的操作。为此的主要工具是 `sum` 函数。它使您能够计算数组中每个元素的总和，或沿特定多维数组的维度计算总和。

设 A 为一个数组，其元素为 [5 6 7 8 9]。

您可以使用以下方式的 `sum` 函数来获取该数组所有元素的总和：

输出

在此，使用 `sum` 函数将数组 A 的成员相加，得出总和为 35。在 MATLAB 中，更复杂的求和任务都建立在此基本技术之上。

累积和

此外，MATLAB 还提供了一种便捷的方法，通过利用 `cumsum` 函数来计算数组元素的累积和。使用此方法，会创建一个新数组，该数组的每个元素都是原始数组中到该点为止所有元素的总和。

考虑数组 A，其元素为 [1 2 3 4 5]。

您可以使用 `cumsum` 函数按以下方式查找元素的累积和：

输出

在这种情况下，通过将 [1 2 3 4 5] 的累积总和相加，会产生数组 [1 3 6 10 15]，其中每个元素都代表原始数组中直到该位置的相应元素的总和。

定积分

MATLAB 中的 `integral` 函数用于计算函数在给定区间上的定积分。借助此函数，用户可以执行数值积分，以确定特定范围内连续函数的累积值或曲线下的面积。定积分是微积分中的一个基本概念，MATLAB 的 `integral` 函数可以轻松地对各种函数的这些积分进行数值计算。

`integral` 函数的一般语法如下：

例如，假设您希望计算函数 f(x)=x*2 的定积分，并且您有一个函数。

以下是对构成 `integral` 函数的每个元素的详细解释：

Q：这代表定积分的数值。它给出了在区间 [a, b] 上给定函数的曲线下的面积或累积值。

fun：这是需要积分的函数。它可以定义为函数句柄，使用 `@(x)` 表示法，或者内联定义。

a 和 b：参数 a 和 b 分别界定了定积分的下限和上限。它们定义了要执行积分的时间段。

可以按以下方式应用 `integral` 函数：

输出

在此示例中，使用 `integral` 函数计算了函数 f(x)=2x 在 [0, 1] 区间上的定积分，得到数值 1/3，约等于 0.3333。这说明了 `integral` 函数如何用于执行各种函数类型的数值积分，并在 MATLAB 中提供精确的定积分结果。

带可选参数的求和

MATLAB 的 `sum` 函数有几个可选参数，可在处理数组和执行特定求和操作时提供更多灵活性。这些参数包括数组的无穷大和 NaN（非数字）值，以及求和进行的维度。沿特定维度的求和

在多维数组操作中，可能需要沿特定维度计算总和。您可以使用 `sum` 函数指定要执行求和的维度。

C = [1 2 3; 4 5 6; 7 8 9];

可以使用以下语法找到沿行（维度 1）的元素总和：

输出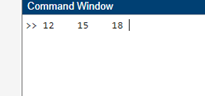

处理无穷大和 NaN

MATLAB 提供了选项来处理求和过程中的无穷大和 NaN 值。使用 'include' 选项，您可以选择包含或排除 NaN 值。类似地，根据 'omitinf' 和 'includeinf' 选项，在求和过程中对无穷大的处理方式有所不同。

假设您有一个包含 NaN 和无穷大值的数组 D。

您可以使用 'omitnan' 参数按以下方式计算总和，同时忽略 NaN 值：sum_without_nan = sum(D, 'omitnan');

输出

7

此处，`sum` 函数计算数组 D 中元素的总和，排除了 NaN 值，得到总和为 7。