Z 变换

引言

Z变换是数字信号处理和控制系统领域的重要工具，它是一种定义，能够分析和设计离散时间系统。它将离散时间信号（通常由一系列数字描述）转换为频域。这种转换特别有价值，因为它简化了系统的分析和设计，将时域卷积运算转换为Z域中的乘法。

数学上，离散时间信号x[n]的Z变换定义为

其中

• x[n]是离散时间信号。
• z是一个复变量，表示为z = re^jω，其中r是幅值，ω是角度（频率分量）。

Z变换的多功能性体现在它能够像傅里叶变换一样从频率角度分析系统，但其额外优势在于能够处理不一定是正弦的输入信号和时域系统。

历史背景和发展

Z变换于20世纪中叶引入，建立在早期使用拉普拉斯变换分析连续时间系统的基础上。这种变换由与连续时间系统的拉普拉斯变换相同的皮埃尔-西蒙·拉普拉斯开发，专门用于解决离散时间系统中的问题。这是为了响应20世纪50年代和60年代数字计算机和数字信号处理的兴起，标志着该领域的一个重大转变。

在信号处理和系统理论中的重要性

Z变换由于能够简化复杂操作并提供对系统行为的洞察，因此在信号处理和系统理论中发挥着至关重要的作用。

• 卷积的简化： 在时域中，两个序列的卷积是一个相当复杂的过程。另一方面，在Z域中，卷积比乘法简单得多，这使得使用这种方法分析和设计系统成为可能。
• 系统稳定性分析： 在Z变换中，我们可以找到系统的极点，并根据这些极点判断系统是否稳定。如果系统的所有极点都位于Z平面单位圆内，则称系统是稳定的。
• 频率响应分析： 系统的频率响应可以通过评估单位圆上的Z变换来确定，因为Z变换关注系统在n的整数值处的性质：|z| = 1。
• 滤波器设计： 数字滤波器是即使是最简单的数字信号处理系统的核心组件，Z变换在这些滤波器的设计中得到了大量提及。它们用于消除噪声、提升感兴趣信号的特定特性以及执行其他信号调节操作。

与其他变换的比较

Z变换在某种程度上类似于傅里叶变换和拉普拉斯变换，因为它源自它们，但在离散时间系统中是有益的。

• 傅里叶变换： 傅里叶变换是分析连续时间信号并将其转换为频率分量的主要工具。如果Z变换在单位圆上（z = ejω），则Z变换可以被认为是离散时间傅里叶变换（DTFT）的推广。然而，与始终假设正弦输入信号的DTFT不同，Z变换允许检查具有指数傅里叶系数并因此具有指数增长或衰减的信号。
• 拉普拉斯变换： 拉普拉斯变换用于连续时间模型，即将信号转换到“s”域后。Z变换类似于拉普拉斯变换，但适用于离散时间信号。它们中的每一个都使得可以从对系统稳定性和频率特性很重要的极点和零点角度考虑系统。拉普拉斯变换只涉及一个复变量s = σ + jω，而Z变换涉及z = re^jω。Z变换是拉普拉斯变换的离散时间模拟。

数学基础

离散时间序列

离散时间序列被定义为一组由整数标记的数字，其中每个数字可以表示信号在某个时间点的实例。在数学上，离散时间序列可以表示为

x[n] = {x[n]}，n ϵ Z

其中

• x[n]表示序列在整数索引n处的值。
• n可以取任何整数值，表示序列中的样本号。

离散时间序列代表了一类重要的信号，并广泛用于数字信号处理和控制系统中，其中信号基本上是采样保持型。这些序列是Z变换的输入，Z变换将它们转换为复函数，然后用于进一步分析。

Z变换的收敛性

Z变换仅对满足收敛准则的z值收敛。已经发现，每个此类定义的级数的Z变换仅在该级数的绝对值之和有限时收敛

Z变换对所有给定序列可求和的z值收敛，那么所有这些z值的集合称为收敛域（ROC）。ROC也用于理解序列所呈现的系统行为和稳定性。

收敛域 (ROC)

收敛域是Z平面上Z变换收敛的z值集合。ROC的定量定义是：对于二元分类器，ROC由以下数学公式确定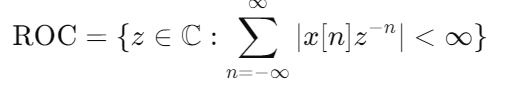

ROC至关重要有几个原因

• 它被发现有助于定义Z变换的存在。
• 它提供了关于系统稳定性的信息；例如，对于因果系统，ROC位于复平面中圆的外部。
• ROC也用于分析系统的稳定性、因果性或反因果性。

ROC在系统稳定性方面的作用

系统稳定性可以使用ROC进行分析

• 稳定系统：如果ROC是单位圆|z| = 1，则系统是稳定的，因为随着时间趋于无穷大，输出不会趋于无穷大。
• 因果系统：在因果系统中，ROC是从有限值[r]到无穷大[即，|z| > r]。
• 反因果系统：对于反因果系统，ROC位于半径为'r'的圆内（即|z| < r）。

稳定性也由ROC与单位圆之间的距离决定，距离越大，数字系统的稳定性越高。如果单位圆在ROC内，则所涉及的系统是稳定的；否则，系统是不稳定的。

Z变换的性质

这些性质使得复杂的信号处理任务和系统分析成为可能。

1. 线性

Z变换通常是线性算子，因此它遵循叠加原理。如果x1[n]和x2[n]是两个独立的离散时间序列，其Z变换分别为x1->X1(z)和x2->X2(z)，并且存在常数a和b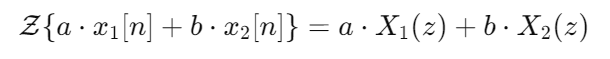

2. 时移

时移可以描述为信号通过大量或少量样本进行计时。对于序列x[n]，其Z变换为X(z)，则x[n-k]或偏移'k'个样本的序列的Z变换为

时移在系统分析中非常重要，例如，在分析带有延迟器的系统（如数字滤波器）时。该属性使工程师能够预测输入信号在时间上向前或向后移动时系统的行为。

3. 卷积

时域中的卷积等于Z域中的乘法。当第一个时序是x1[n]，第二个时序是x2[n]时，为了得到y[n] = x1[n] * x2[n]的序列，这两个序列之间的卷积具有Z变换

Y(z) = X₁(z) . X₂(z)

在系统理论中，当需要计算LTI系统在给定输入信号和系统脉冲响应时的响应时，该性质被广泛使用。该性质在分析系统行为时很有帮助，因为它将卷积运算转换为Z域中的乘法。

4. Z域微分

Z域中的微分与时域中乘以n相关。如果X(z)是x[n]的Z变换，则n * x[n]的Z变换表示为

该性质有助于检查遇到随时间线性增加的斜坡函数的系统行为。它用于在Z域中操纵信号，从而有助于求解微分方程和分析系统行为。

5. 初值和终值定理

初值定理

初值定理用于从其Z变换X(z)确定原始序列x[n]的初值，而无需进行逆Z变换。该定理指出

终值定理

终值定理用于在n趋近无穷大时找到序列x[n]的稳态值。如果(1-z^-1)X(z)的所有极点都在单位圆内，则该定理适用

逆Z变换

逆Z变换是一种用于离散时间信号处理系统的方法，用于获取Z域函数的时域响应。与Z变换相反，Z变换将离散时间序列映射到Z域，并且在识别线性时不变 (LTI) 系统（尤其是在数字信号处理和控制系统中）方面非常有用。

离散时间序列x[n]的Z变换的表示法定义为

为了从X(z)获得原始序列x[n]，我们应用逆Z变换

[ x[n] = 逆Z变换{X(z)}

逆Z变换的解不唯一；至少有两种方法可以根据X(z)和收敛域计算函数。

逆Z变换的方法

1. 长除法

在长除法中，当X(z)表示为有理函数形式时，X(z)的分子被分母除。如果X(z)是一个简单的有理函数，并且只需要生成序列的少量项，则此方法相对简单且最有效。

步骤：

• 这可以使X(z)表示为有理函数，X(z) = N(z)/D(z)。
• 使用特殊的对数除法将N(z)除以D(z)，以获得z的商和余数。
• 存储幂次递减的项（）以形成序列x[n]。

2. 部分分式展开

部分分式展开是计算有理函数逆Z变换最有效的方法之一。它简单地将X(z)分解为更简单的形式，其中各个项可以与标准Z变换对关联。

步骤：

• 写出X(z) =C 1 / [z(2 − z) + 2 uz] + C 2 / [z(z + 2) + 2 uz] + C 3 / [(z + 2) + 2 uz]。
• 通过使用已学习的Z变换对，确定每个分数的逆Z变换。
• 最终结果x[n]是单个脉冲和两个变换输出的逆变换之和。

3. 残留法

残留法利用复变函数分析和围道积分的残数理论来确定逆Z变换。它在其他方法可能出现问题的更复杂计算中很有用。

步骤：

• 写出X(z)的表达式，以便可以对其拉普拉斯变换进行积分。
• 使用逆z变换公式和围绕X(z)的零点和极点的围道积分。
• 为了确定序列x[n]的项，需要计算每个极点处的残数。

4. 幂级数展开

幂级数展开与X(z)的幂（z-1）表示相关。如果函数X(z)可以以某种自然方式展开成级数，则此方法非常宝贵。

步骤：

• 将X(z)写成z-1的幂级数形式。
• 将z-n的系数定义为时域序列x[n]。

Z变换在系统分析中的应用

Z变换广泛用于分析和设计离散时间系统，这些系统在信号处理和控制工程中非常常见。通过将序列转换为Z域，可以轻松操纵和分析这些系统的特性、稳定性和响应。

传递函数表示

差分方程可以表示离散时间LTI。通过这种方式，如果将Z变换应用于该差分方程，则可以在Z域中推导出与系统行为相对应的传递函数。传递函数H(Z)也可以定义为H(Z) = Y(Z)/X(Z)，其中Y(Z)和X(Z)分别是Y(n)和X(n)的Z变换。

该传递函数提供了对系统对任何输入序列的响应的洞察。通过查看H(z)，可以观察系统在输入特定值时（例如频率响应）的行为。

传递函数及其解释

传递函数H(z)通常定义为多项式的比率

这里，bi和ai值是系统的特征，如系统的增益和反馈。分子多项式给出系统零点的位置，分母多项式给出系统极点的位置。

• 零点：H(z)为零的z的分布。零点表示系统将输出抑制为零的频率。
• 极点：H(z)函数可能无限大的z值。极点是系统响应最强或最振荡的频率。

系统稳定性分析

离散时间系统的稳定性可以通过Z变换的收敛域分析来评估。ROC是Z变换收敛并取有限值的z距离。如果系统要稳定，则ROC必须包含单位圆，即Z域中的|z| = 1。

• 因果系统： 通常，对于因果系统（其中输出是当前和过去输入而非未来输入的函数），ROC位于最外层极点之外。
• 反因果系统： 我还绘制了反因果系统的ROC，其中输出仅取决于未来输入，并且位于最内层极点之内。
• 双边系统： 在系统既不严格因果也不反因果的情况下，ROC是极点之间的环。

如果ROC包含单位圆，从而暗示任何有界输入的响应也是有界的，则称系统是稳定的。

Z域中的极点-零点分析

系统的稳定性和动态行为也可以通过检查Z域中极点和零点的位置来分析

• 极点： 如果传递函数的所有极点都位于单位圆内（即|z| < 1），则系统是稳定的。如果任何极点至少有一个值在单位圆之外，则所分析的系统是不稳定的。
• 零点： 零点本身对稳定性没有影响，但零点相对于系统中极点的位置有助于系统的频率响应。

极点-零点图通常应被视为评估系统稳定性和其动态性质的有效方法。重要的是，这意味着极点越接近单位圆，系统的响应就越慢，或者换句话说，其衰减所需的时间就越长。

离散时间系统分析

离散时间LTI系统交汇点

离散时间LTI系统在数字信号处理和控制系统中至关重要。通常，使用Z变换分析此类系统包括确定所考虑系统对输入信号产生的响应类型。

通过获取系统的传递函数H(z)，

• 脉冲响应： 这是系统对离散时间脉冲的响应，有时也称为系统的脉冲响应，通常称为克罗内克-德尔塔函数。H(z)是其脉冲响应具有Z变换S(z)的系统的传递函数。
• 阶跃响应： 系统的阶跃响应描述了系统对阶跃输入的反应。因此，阶跃响应可以确定为函数H(z)/[1-(z^-1)]的逆Z变换。
• 频率响应： 系统在正弦输入存在时的行为。这是通过评估单位圆上z = e^jω处的H(z)获得的。

使用Z变换进行滤波和系统稳定性示例。

数字滤波器广泛应用于音频信号、电信系统和图像处理等各种应用中。在数字滤波器设计中最流行的变换是Z变换。

• 低通滤波器： 允许低频信号通过而抑制高频信号的滤波器。也就是说，一个简单的低通滤波器的传递函数可以表示为
  
• 高通滤波器： 电路中只允许高频信号通过并衰减低频信号的组件。传递函数可能如下所示
  

因此，从这些滤波器的极点和零点可以确定它们的稳定性和频率响应。例如，滤波器的稳定性取决于系统的极点是否位于单位圆内。

Z变换的应用

1. 数字信号处理 (DSP)

滤波器是DSP的基本构建块，用于根据需要操纵或修改信号。由于许多物理滤波器可以大致分为有限脉冲响应（FIR）或无限脉冲响应（IIR），因此这些滤波器根据预期应用而广泛使用。

2. Z变换在图像处理中的应用

在图像处理中，Z变换用于分析和设计信号，以实现图像增强、复原和图像压缩。由于图像可以被视为二维信号，因此Z变换也可以扩展到二维以进行处理。

3. 控制系统

数字控制系统用于处理电机、机器人、工业、流程等控制和动态系统。与模拟系统相比，数字控制系统包含离散时间信号。

4. 通信系统

在通信系统中，信号通过某些介质传输，调制在传输这些信号中起着至关重要的作用。Z变换应用于数字电路中的调制和解调，因为这些方法可以有效地转换为数字域。

通过利用Z变换，可以了解调制如何影响信号的频谱。工程师可以通过在Z域中检查调制信号来设计能够最大化带宽利用率并最小化干扰的系统。

结论

Z变换对于离散时间系统分析和设计至关重要，尤其是在数字信号处理和控制系统中。Z变换通过将序列转换为Z域，简化了滤波器设计、系统稳定性分析和卷积等领域的复杂计算。