使用 MATLAB 的线性块代码

引言

线性分组码是一类纠错码，旨在通过检测和纠正数字通信信道中可能发生的错误来提高数据质量。在数据传输和信号容易受到干扰导致失真的嘈杂环境中，它们至关重要。线性分组码通过将给定数量的数据位映射到更长的编码位序列来进行纠错，该序列包含校验位，即使某些位发生变化，也能重建原始消息。

线性分组码是编码理论中用于检测和纠正传输系统中错误的入门级编码技术。在这种方法中，k 位的信息消息被映射到 n 位的码字，其中 n > k。额外的开销（冗余）使得能够检测和可能纠正通信过程中发生的错误。

在通信系统中的重要性

成型码是通信系统中最为常见的码，主要用于确保数据传输更可靠且不受错误信号的影响。其应用的重要性体现在 WiFi 和蓝牙等无线信号传输、卫星传输以及对错误敏感度要求极低的数据存储领域。

在信息以块/包形式发送的通信中，线性分组码会在每个包中添加额外的位，使接收器能够检测和纠正特定形式的错误，而无需请求重传。对于实时数据共享应用（如视频流和网络语音通话（VoIP））来说，这种能力非常宝贵，因为延迟对其影响很大。此外，线性分组码可确保在长距离上传输的信号质量良好，如在重传成本高昂的卫星和深空传输中所见。

线性分组码基础

线性分组码是一类纠错码，在给定的通信系统中通常用于检测和纠正传输数据流中固有的错误。线性分组码通过添加额外的位来将消息映射到更长的位串（称为码字），这些额外的位有助于错误检测甚至纠正。

• 码字长度 (n)： 指构成消息的总位数，包括实际数据和代码引入的纠错位数。
• 消息长度 (k)： 指在进行任何编码之前，原始消息中的数据位数。

总而言之，这些码构成 (n, k) 码。其中 `n` 代表消息位数加上为创建能够检测和/或纠错的代码而添加到消息中的奇偶校验位数；`k` 的值始终小于 `n`，即：n - k = 奇偶校验位数。

示例： 在 (7, 4) 码中，n = 7 且 k = 4。这意味着每个码字长 7 位，其中 4 位直接传输消息，其余 3 位用于错误检查。

线性分组码的性质

• 线性： 线性分组码是线性的，任何有效码字之间的线性组合也是有效的。此属性使得编码和解码更简单，因为它是使用 矩阵 进行码字构造的系统化方法。
• 汉明距离： 两个码字之间的汉明距离是指包含不同位的位数。在线性分组码中，最小汉明距离是决定错误检测和纠错能力的决定性因素。根据最小距离 d_min，该码可以检测 d_min - 1 个错误。它还可以纠正多达 ⌊`(d_min - 1) / 2`⌋ 个错误。
• 纠错能力： 奇偶校验位的引入，使得线性分组码能够检测和纠正错误。码的纠错能力随着最小汉明距离的增加而提高。在具有较大最小距离的情况下，该码具有更好的纠错能力，但对于特定的消息长度 (k)，码字长度 (n) 会更长。

线性分组码的类型

• 汉明码： 汉明码是最流行的线性分组码之一，能够纠正单个错误。它们易于使用，最小汉明距离为 3，该码可以检测多达 2 个错误并纠正每个码字中的 1 个错误。汉明码可以表示为 ( 2^m - 1, 2^m - m -1)，其中 m 是与数据消息位数相关的额外位数。例如，(7, 4) 汉明码可以纠正一位错误。
• 循环码： 循环码是线性分组码的一个子类，其中对码字进行移位会产生另一个允许的码字。因此，它们可以在通信系统的硬件中轻松实现。 错误检测 的一个典型例子是 CRC，也称为循环冗余校验。
• 里德-所罗门码： RS 码是数据存储、卫星和 CD/DVD 错误校正中最实用的分组码之一。RS 码是非二进制码。也就是说，它们是按符号而不是按位工作的。它们在纠正突发错误方面非常高效。这些码可以在码字内纠正多达 `t` 个符号错误，具体数量由码参数定义。

线性分组码的数学基础

线性分组码在数字通信领域的错误检测和纠错中得到广泛应用。为了确保准确捕获信号，这些码依赖于结构化的技术，主要使用矩阵来创建可靠的数据编码/解码机制。

1. 生成矩阵 (G)

生成矩阵 G 是生成线性分组码的关键特征，因为它对输入消息进行编码并产生称为码字的代码输出。在 (n, k) 线性分组码中

• k 代表消息（输入数据）的位数。
• N 代表码字（输出数据）的位数。

线性分组码是基于向量空间构建的，这意味着形成的任何码字都是由 G 的行组成的。

构造生成矩阵

• 一个 ( n, k ) 码的生成矩阵 G 包含 k 行，每行有 n 列。
• G 通常以系统形式构造，分为两部分
• 左侧有一个 k × k 的单位矩阵 I_k。
• 右侧是变换 θ 后的 k ×(n - k) 奇偶校验矩阵 P。

例如，(7,4) 码（如汉明码）的生成矩阵形式如下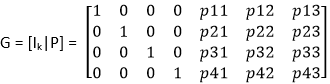

在 MATLAB 中，您可以这样构造 G：

• 使用 G 对消息进行编码： m 是长度为 k 的二进制向量，乘以 G

在 MATLAB 中

2. 奇偶校验矩阵 (H)

奇偶校验矩阵 H 用于检查和纠正接收到的码字中的错误。它在线性分组码的解码过程中使用，是现代通信系统中不可或缺的一部分。

构造奇偶校验矩阵

• 对于 (n, k) 码，H 是一个 (n − k) × n 矩阵。
• H 通常结构如下
• 上述方程中 H 的右侧是 In-k 单位矩阵。
• H 的左侧是 G 中奇偶校验矩阵 P 的转置。

例如，对于 (7, 4) 汉明码，如果 P 如上定义，则 H 可以构造为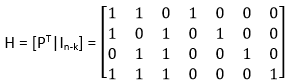

在 MATLAB 中

• H 在错误检测中的作用： 当接收到的码字 r 与 HT 相乘时，产生的（伴随式 s）值可以指示错误的发生。

在 MATLAB 中

3. 编码和解码过程

G 和 H 是一组函数，用于实现编码和解码过程，以优化消息到码字的映射以及检测错误或纠正接收到的数据。

编码

• 从二进制消息向量 m 开始。
• 要创建码字 c，消息 m 乘以生成矩阵 G。

解码

• 当接收到码字时，将其乘以 HT 以得到伴随式。
• 当 s = 0 时，可能没有错误。
• 如果 s ≠ 0，则有关于错误位置的信息。因此，可以纠正单个振荡错误。

• 错误纠正： 例如，对于汉明码，伴随式直接指向码字中的错误位置。在这种情况下，必须翻转指定为错误位置的相应位。

在 MATLAB 中实现线性分组码

MATLAB 编码理论配置

要模拟线性分组码，需要在 MATLAB 环境中调整编码理论所需的工具。MATLAB 包含丰富的通信工具箱，提供了各种函数，用于线性分组码的构建、模拟和分析。

通信工具箱

• 安装工具箱：您首先需要确保拥有通信工具箱。如果没有，可以通过 MATLAB 附加管理器屏幕添加。
• 选择附加组件，然后选择获取附加组件并键入“通信工具箱”。
• 安装：在设置窗口中使用箭头键单击安装。
• 要进入文档，在 MATLAB 窗口中输入：

可用于线性分组码的关键函数包括 encode、decode、given to parallel、parallel to given，以及构建 stable 的功能，等等。

MATLAB 工作区准备

• 打开一个新的 MATLAB 脚本，以便您的代码结构更清晰；您还应该调用所需的任何库。
• 编写分组编码方程，然后定义分组编码方程中使用的参数，例如代码长度 (`n`)、消息长度 `k` 以及要使用的任何矩阵。

MATLAB 中的编码

在线性分组编码中，编码过程涉及生成生成矩阵 (G)，该矩阵使消息能够转换为要编码的码字。

编码分步指南

1. 定义代码参数

我们可以选择 `n`（码字长度）和 `k`（消息长度）的值。例如，汉明 (7, 4) 码的原始值为 `n = 7，消息字符串长度为 k = 4。

然而，计算码率作为比率：R = k/n 来显示代码的有效性。

2. 创建生成矩阵 (G)

对于编码，生成矩阵 `G` 在构造中起着重要作用。它通常结构为

G = [Ik | P]

其中 `I_k` 是 `k x k` 维的单位矩阵，`P` 是提供奇偶校验位的奇偶校验矩阵。

• 示例： 在本例中，构建 (7,4) 汉明码，我们将手动完成或使用 MATLAB 函数

3. 编码消息

通常，如果 k 大于 1，则需要区分两种消息状态；定义一个大小为 1 x k 的消息向量，例如 [1 0 1 1] 进行编码。

G 乘以消息向量得到码字

• 结果是大小为 1 x n 的编码码字。

4. 使用内置 MATLAB 函数

MATLAB 提供了许多函数和资源，可在 MathWorks 提供的通信工具箱中使用，包括用于某些标准代码（如 Bach 或 Hamming）的 'encode'。

MATLAB 中的解码

在解码过程中，接收器使用 H 矩阵来查找接收到的码字中的错误并尝试纠正它们。

解码和错误检测方法

1. 构建奇偶校验矩阵 (H)

生成矩阵与奇偶校验矩阵之间的关系可以直接推导出来，也可以从外部定义。

对于 (7,4) 汉明码，H 可以是

2. 计算伴随式

伴随式旨在纠正接收到的码字中的错误。码字应与 `H^T`（H 的转置）相乘。

正的伴随式表示存在错误。在使用伴随式表的情况下，它还可以定位错误位置。

3. 使用伴随式表纠正错误

MATLAB 可以使用 `syndtable(H)` 来为错误校正创建伴随式表。

通过伴随式 `S` 找到接收码字的纠正

4. 解码纠正后的码字

根据伴随式的结构，在 `S` 中找到错误模式以纠正接收到的码字。

5. 替代解码函数

对于特定代码，MATLAB 提供 `decode` 函数。

汉明 (7,4) 码编码和解码示例

MATLAB 示例，将编码和解码结合在一起

线性分组码在现实系统中的应用

1. 数字通信系统

• 无线通信： 无线信道信号容易受到障碍物、天气和其他无线信号等因素的影响。通过线性分组编码，可以在发送数据之前对其进行编码，从而在一定程度上避免这些问题。
• 卫星通信： 每颗通信卫星都面临重大挑战，例如路径衰减大、天气噪声以及来自其他卫星的潜在干扰信号。线性分组码用于确保在如此定义的距离上传输的数据尽可能精确。

2. 数据存储和错误弹性

• 硬盘和 SSD： 在硬盘 (HDD) 和 SSD 中使用的存储设备采用 BCH 和里德-所罗门码等线性分组码。这些码还可以帮助设备识别和纠正随着使用、温度变化以及数据读取或写入而产生的位级错误。

3. 网络和数据通信

• 网络协议： 这会造成问题，因为在使用 TCP/IP 等协议时，数据包可能需要通过多个路由器和交换机，因此会迅速变得嘈杂，并且某些数据包可能会丢失。
• 互联网传输： 在互联网上传输数据时会发生一些干扰；这包括信号干扰以及由于互联网可用连接性的网络波动而产生的干扰。

结论

总之，线性分组码对于识别和修复数据存储和传输系统中的错误至关重要。用户可以通过使用 MATLAB 提供的强大工具来模拟和实现这些程序，从而提高数据可靠性，检查错误性能，并优化各种实际应用的通信系统。