Matlab mesh()

2025年3月17日 | 阅读 10 分钟

引言

MATLAB 是一个强大的数值计算环境，提供了丰富的可视化函数。其中，mesh() 函数在创建三维数学函数和数据集的可视化方面起着至关重要的作用。该函数在工程、物理和数学等领域特别有价值，在这些领域，在三维空间中表示和理解曲面及函数至关重要。

mesh() 函数概述

MATLAB 中的 mesh() 函数主要用于创建 3D 曲面图。

其基本语法如下：

其中，X 和 Y 是表示网格坐标的矩阵，Z 是表示每个网格点高度或函数值的矩阵。让我们深入探讨 mesh() 函数的关键方面和功能。

基本 3D 曲面图

mesh() 函数的基本目的是生成 3D 曲面图。

请看以下示例

% Define a simple surface function
[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = X.^2 + Y.^2;

% Create a mesh plot
mesh(X, Y, Z);

输出

在此示例中，meshgrid() 用于创建 X 和 Y 坐标网格，Z 基于简单的数学表达式计算得出。然后，mesh() 函数可视化该曲面。

自定义图形

MATLAB 的 mesh() 函数允许进行广泛的自定义，以增强曲面图的视觉表示。用户可以修改颜色、着色和光照等方面，以根据其特定需求量身定制可视化效果。

例如

% Customizing the mesh plot
figure;
mesh(X, Y, Z, 'FaceColor,' 'interp,' 'EdgeColor,' 'k,' 'LineWidth,' 1.5);
title('Customized Mesh Plot');
xlabel('X-axis');
ylabel('Y-axis');
label('Z-axis');

输出

此示例演示了如何将面颜色设置为插值，调整边颜色，并指定线宽，从而提供更精细、更具信息量的可视化效果。

叠加多个曲面

mesh() 函数支持叠加多个曲面，从而可以在同一图形中比较不同的数据集或函数。这可以通过多次使用不同的数据矩阵调用函数或使用 hold-on 和 hold-off 命令来实现。

示例

% Overlaying multiple surfaces
figure;
mesh(X, Y, Z);
hold on;

% Define another surface function
Z2 = sin(sqrt(X.^2 + Y.^2));

% Overlay the second surface
mesh(X, Y, Z2, 'FaceColor,' 'none,' 'EdgeColor,' 'r,' 'LineWidth,' 1.5);

hold off;

输出

此代码叠加了两个具有不同函数的曲面，从而清晰地比较它们。

带网格的等高线图

mesh() 函数可以与等高线图结合，创建混合可视化，同时显示曲面和等高线。这对于深入了解数据结构非常有用。

示例

% Creating a mesh plot with contours
figure;
mesh(X, Y, Z);
hold on;
contour(X, Y, Z, 'LineColor,' 'k,' 'LineWidth,' 1.5);
hold off;

输出

在这种情况下，contour() 函数与 mesh() 一起使用，以在 3D 曲面图上显示等高线。

Meshgrid 和坐标变换

meshgrid() 与 mesh() 函数的结合使用对于创建 3D 绘图所需的坐标网格至关重要。理解如何操作这些网格坐标对于有效可视化至关重要。

示例

% Meshgrid and coordinate transformations
[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = X.^2 + Y.^2;

% Perform coordinate transformation
theta = pi/4;
X_rot = X * cos(theta) - Y * sin(theta);
Y_rot = X * sin(theta) + Y * cos(theta);

% Create a mesh plot with transformed coordinates
figure;
mesh(X_rot, Y_rot, Z);

输出

此示例演示了如何执行简单的坐标变换并可视化修改后的曲面。

MATLAB 中的 mesh() 函数是创建引人注目的 3D 曲面可视化对象的强大工具。
其多功能性使用户能够表示复杂的数学函数、比较数据集，并深入了解其数据的结构。
通过了解各种自定义选项、叠加多个曲面、与等高线图结合以及使用 mesh grid () 操作网格坐标，用户可以充分利用 mesh() 函数在三维空间中进行有效数据分析和可视化的全部潜力。
无论您是工程师、科学家还是研究人员，掌握 mesh() 的功能都可以显著提高您在视觉上交流和解释复杂信息的能力。
此示例演示了如何执行简单的坐标变换并可视化修改后的曲面。

透明度和面 Alpha

mesh() 函数允许用户在图形中加入透明度。这可以通过调整 FaceAlpha 属性来实现。

示例

% Cr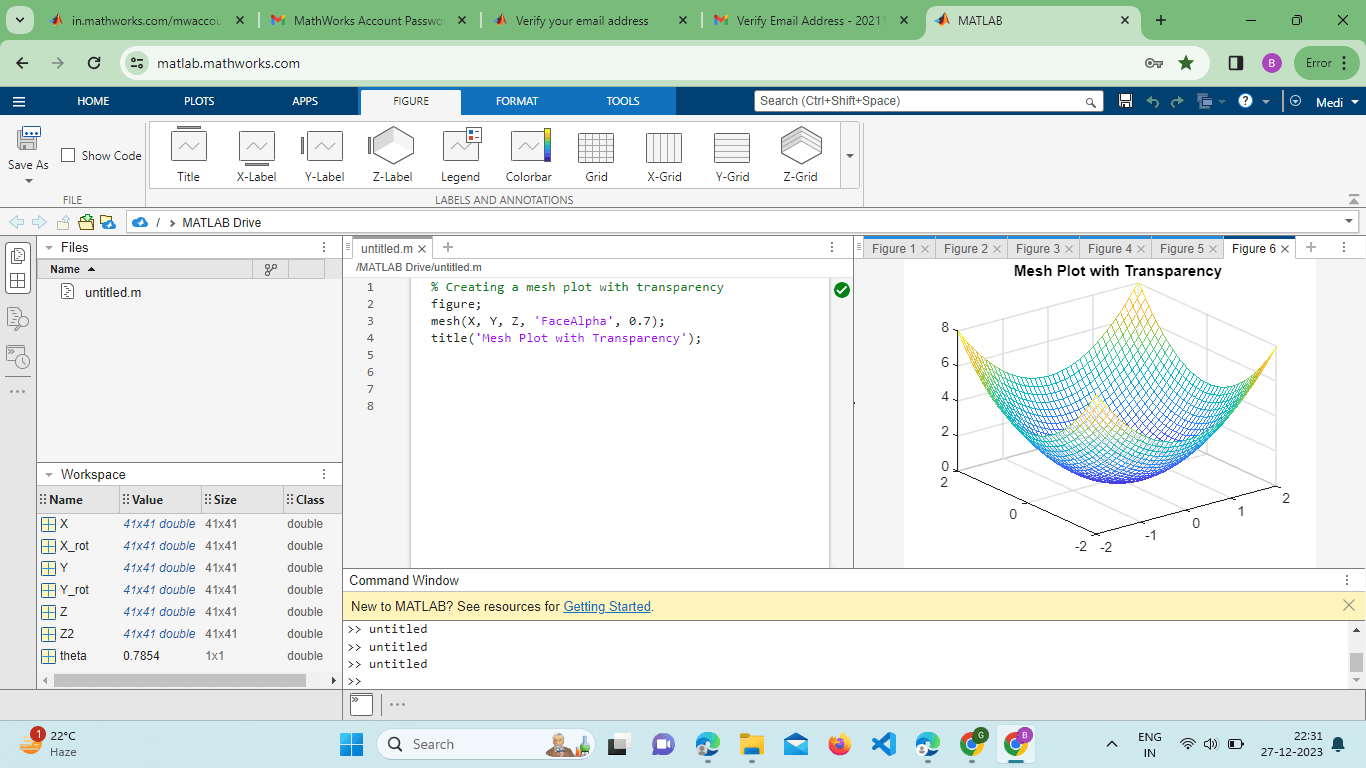eating a mesh plot with transparency
figure;
mesh(X, Y, Z, 'FaceAlpha', 0.7);
title('Mesh Plot with Transparency');

输出

FaceAlpha 属性的范围从 0（完全透明）到 1（完全不透明），提供了一种揭示底层结构或模式的方法。

使用 Quiver3 可视化梯度

对于包含矢量场的数据集，可以结合使用 quiver3() 函数和 mesh() 函数来可视化每个点的梯度或流动方向。

示例

% Vi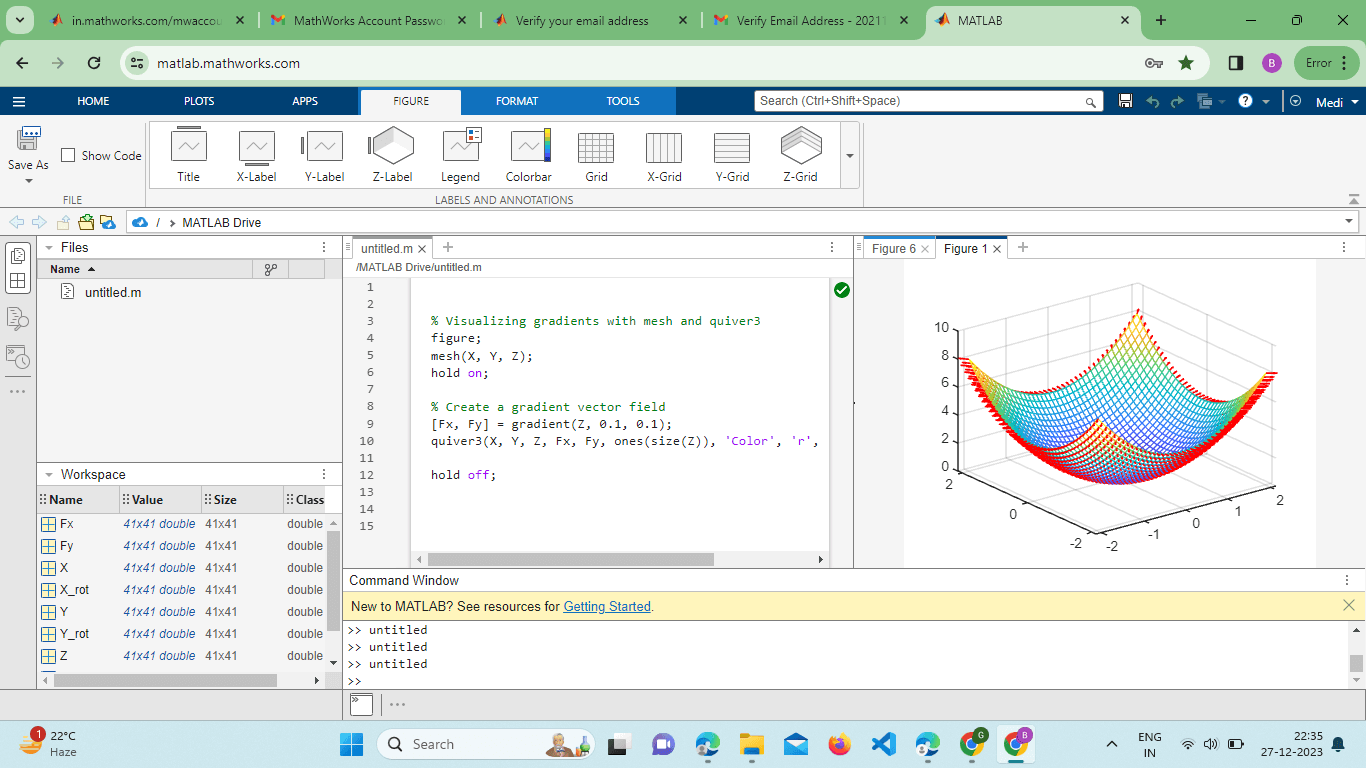sualizing gradients with mesh and quiver3
figure;
mesh(X, Y, Z);
hold on;

% Create a gradient vector field
[Fx, Fy] = gradient(Z, 0.1, 0.1);
quiver3(X, Y, Z, Fx, Fy, ones(size(Z)), 'Color,' 'r,' 'LineWidth,' 1.2);

hold off;

输出

此代码将 3D 曲面图与描述每个点处梯度方向的 quiver 图叠加在一起。

参数曲面

mesh() 函数可以通过定义 X、Y 和 Z 的显式参数方程来可视化参数曲面。

示例

% Parametric surface using mesh
u = linspace(0, 2*pi, 100);
v = linspace(0, pi, 50);
[U, V] = meshgrid(u, v);

% Parametric equations for a torus
R = 2; r = 1;
X = (R + r*cos(V)) .* cos(U);
Y = (R + r*cos(V)) .* sin(U);
Z = r * sin(V);

% Create a mesh plot for the torus
figure;
mesh(X, Y, Z);

输出

本例展示了如何使用参数方程生成一个环面并使用 mesh() 函数进行可视化。

使用 Rotate3d 进行交互式探索

MATLAB 提供了交互式工具来探索 3D 图形。rotate3d 函数使用户能够交互地旋转和平移图形，从而更全面地理解数据。

示例

% Interactive exploration with rotate3d
figure;
mesh(X, Y, Z);
title('Interactive 3D Plot');
rotate3d on; % Enable interactive rotation

输出

激活 rotate3d 工具允许用户自由旋转图形，从而动态地查看 3D 曲面。

导出图形

MATLAB 的 mesh() 图形可以导出为各种文件格式，以便包含在报告或演示文稿中。saveas 函数是此目的的便捷工具。

% Exporting the mesh plot as a PNG file
figure;
mesh(X, Y, Z);
title('Exporting Mesh Plot');
saveas(gcf, 'mesh_plot.png');

输出

此示例演示了如何使用散点插值来创建更平滑的曲面表示。

曲面切片和截面分析

MATLAB 的 mesh() 函数可以与切片技术结合使用，以揭示内部结构或分析 3D 曲面的截面。slice 函数通常用于此目的。

% Surface slicing and section analysis
figure;
mesh(X, Y, Z);
hold on;
% Define a slicing plane
slice_plane = surf([0 0; 0 0], [min(Y(:)) max(Y(:)); min(Y(:)) max(Y(:))], [min(Z(:)) min(Z(:)); max(Z(:)) max(Z(:))], 'FaceAlpha', 0.5);
hold off;

输出

此示例演示了如何使用 slice 函数创建切片平面并分析 3D 曲面的截面。

与其他图形类型的集成

mesh() 函数可以与其他 MATLAB 绘图函数无缝集成，以创建全面的可视化效果。例如，将 plot3 与 mesh() 结合使用，用户可以在 3D 曲面上叠加线图。

% Integrating mesh with plot3
figure;
mesh(X, Y, Z);
hold on;
% Assume you have a line plot defined by X_line, Y_line, Z_line
plot3(X_line, Y_line, Z_line, 'r', 'LineWidth', 2);
hold off;

输出

本例展示了线图与 3D 曲面图的集成，以获得更全面的可视化效果。

使用外部颜色图

MATLAB 的 mesh() 函数支持使用外部颜色图来增强曲面的视觉表示。可以使用颜色图来表示其他信息，如温度、应力或浓度。

示例

% Applying an external colormap to mesh
figure;
mesh(X, Y, Z);
colormap('parula'); % Use the parula colormap
colorbar;

输出

此示例演示了如何将 'parula' 颜色图应用于 mesh 图，从而为 Z 值提供颜色比例。

叠加多个曲面

mesh() 函数支持叠加多个曲面，从而可以在同一图形中比较不同的数据集或函数。这可以通过多次使用不同的数据矩阵调用函数或使用 hold-on 和 hold-off 命令来实现。

示例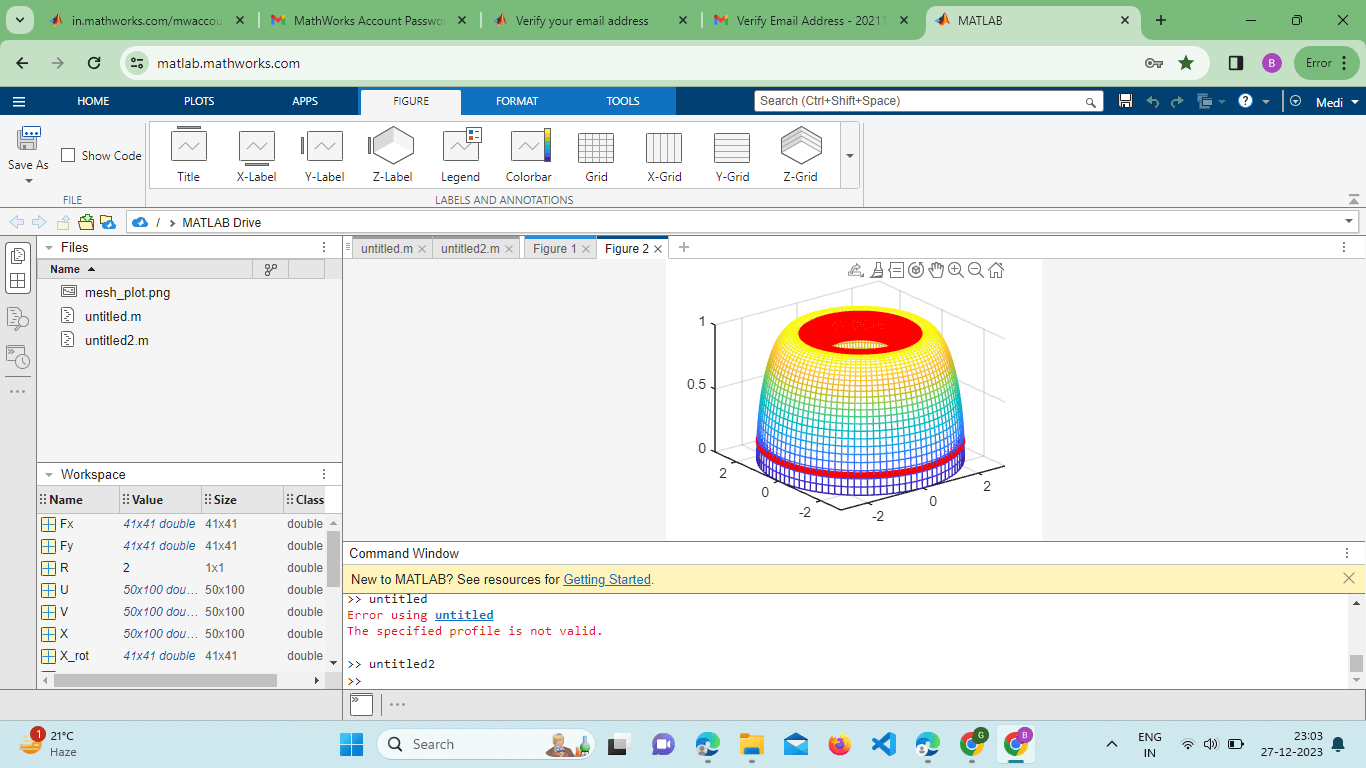

在 MATLAB 中使用 mesh() 函数叠加多个曲面是一种在同一图形中比较不同数据集或函数的强大技术。

让我们更详细地探讨这个主题。

示例

% Generating data for two surfaces
[X, Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z1 = peaks(X, Y);
Z2 = 0.5 * peaks(X, Y);
% Plotting the first surface
figure;
mesh(X, Y, Z1);
title('Overlaying Multiple Surfaces');
xlabel('X-axis');
ylabel('Y-axis');
label('Z-axis');
grid on;
% Overlaying the second surface
hold on;
mesh(X, Y, Z2, 'FaceColor,' 'r,' 'EdgeColor,' 'none');
hold off;
% Adding a legend
legend('Surface 1', 'Surface 2');
% Adjusting the view for better visibility
View(30, 40);

输出

说明

我们使用 peaks 函数生成两个曲面 (Z1 和 Z2) 的数据。第一个曲面 (Z1) 使用 mesh() 函数绘制。我们使用 hold-on 来保留当前图形，同时添加具有不同颜色且无边缘颜色的第二个曲面 (Z2)。使用 legend 函数来区分两个曲面。最后，我们使用 view 函数调整视图以获得更好的可见性。

MATLAB 中的 mesh() 函数被证明是一种极其通用的 3D 可视化工具，提供了多种高级功能和技术。

无论是曲面平滑、动画、切片、与其他图形类型的集成，还是应用外部颜色图，MATLAB 都为研究人员和工程师提供了一个全面的环境来创建复杂且信息丰富的可视化。
随着用户继续探索和试验这些高级功能，他们可以量身定制可视化效果以应对特定挑战，并清晰深入地传达复杂信息。
mesh() 函数的灵活性和可扩展性使其成为 MATLAB 中复杂 3D 数据表示的基石。

使用 MATLAB 的 mesh() 函数的优点

易用性：MATLAB 的 mesh() 函数是 MATLAB 绘图库的一部分，使其易于访问且用户友好。语法简单，用户只需少量代码即可创建 3D 曲面图。

多功能性：mesh() 函数功能多样，可以处理各种数学函数和数据集。它支持参数曲面和散点数据，并可与其他 MATLAB 函数结合用于高级可视化。

自定义：MATLAB 为 mesh() 图形提供了广泛的自定义选项。用户可以调整颜色、着色、线型等，以根据特定需求量身定制视觉表示。这种灵活性对于有效传达信息至关重要。

与其他 MATLAB 函数集成：mesh() 与 quiver3()、contour() 和 plot3() 等其他 MATLAB 绘图函数无缝集成。这种集成使用户能够创建结合多种信息类型的复杂可视化。

交互式探索：mesh() 函数可以与 rotate3d 和数据游标模式等交互式工具结合使用，使用户能够动态地探索 3D 图形。这种交互式功能增强了用户理解复杂数据的能力。

动画支持：MATLAB 支持 mesh() 图形的动画，使您能够可视化数据随时间的变化。这对于传达科学和工程应用中的动态过程和趋势很有价值。

导出功能：MATLAB 支持将 mesh() 图形导出为各种文件格式，如 PNG、JPEG 甚至视频文件。此功能对于将可视化内容包含在报告、演示文稿或出版物中至关重要。

插值和平滑：mesh() 函数可以与插值技术（如 grid data()）结合使用，以从稀疏或嘈杂的数据创建更平滑的曲面。这在使用真实世界数据集时非常有利。

截面分析：mesh() 可以与切片技术（如 slice() 函数）结合使用进行截面分析。此功能有利于检查 3D 曲面的内部结构。

使用 MATLAB 的 mesh() 函数的缺点

3D 图形类型有限：虽然 mesh() 在可视化曲面方面功能强大，但在表示某些类型的数据（如体数据）方面可能不够好。对于更专业的可视化，其他函数（如 isosurface）可能更合适。

性能考虑：生成具有大型数据集或复杂参数曲面的复杂 mesh() 图形可能计算量很大。这可能导致性能问题，尤其是在处理大量数据或实时数据时。

高级功能学习曲线：虽然基本用法很简单，但要掌握参数曲面、动画和交互式探索等高级功能可能需要学习过程。用户可能需要时间和练习才能有效利用这些功能。

依赖于 MATLAB：mesh() 函数特定于 MATLAB，这意味着任何查看或重现可视化的人都需要访问 MATLAB 或 MATLAB 查看器。如果需要与没有 MATLAB 的人进行协作或共享，这可能是一个限制。

某些功能的代码复杂性：实现某些高级功能（如带有滑块的动态切片或复杂的参数曲面）可能会导致代码结构复杂。对于初学者或不熟悉 MATLAB 绘图功能的用户来说，这种复杂性可能具有挑战性。

3D 交互控件有限：虽然 rotate3d 支持基本的 3D 交互，但可能缺少专用 3D 可视化工具中的更高级功能。寻求高度交互式和沉浸式体验的用户可能会发现 MATLAB 的内置功能不够。

信息重叠的可能性：在单个 mesh() 图形上叠加多个曲面或信息类型可能会导致视觉混乱或元素重叠，从而可能使可视化效果难以解释。

MATLAB 的 mesh() 函数提供了广泛的优势，使其成为各个领域 3D 可视化的宝贵工具。
但是，用户应注意其局限性，尤其是在处理大型或专业数据集时。
考虑项目的具体需求并探索其他 MATLAB 3D 可视化函数可能有助于缓解其中一些限制。

下一主题MATLAB 中的颜色

Matlab mesh()

引言

mesh() 函数概述

基本 3D 曲面图

自定义图形

叠加多个曲面

带网格的等高线图

Meshgrid 和坐标变换

透明度和面 Alpha

使用 Quiver3 可视化梯度

使用 Rotate3d 进行交互式探索

导出图形

曲面切片和截面分析

与其他图形类型的集成

使用外部颜色图

叠加多个曲面

使用 MATLAB 的 mesh() 函数的优点

使用 MATLAB 的 mesh() 函数的缺点

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

MATLAB 3D 绘图

面试题

MATLAB 杂项

MATLAB 程序

MATLAB GUI

数值积分

MATLAB 多项式

符号数学

线性代数

MATLAB 教程

MATLAB 2D 绘图

MATLAB 图形

数组 & 函数

程序终止

语句 - try, catch

MATLAB 循环

控制语句

Matlab mesh()

引言

mesh() 函数概述

基本 3D 曲面图

自定义图形

叠加多个曲面

带网格的等高线图

Meshgrid 和坐标变换

透明度和面 Alpha

使用 Quiver3 可视化梯度

使用 Rotate3d 进行交互式探索

导出图形

曲面切片和截面分析

与其他图形类型的集成

使用外部颜色图

叠加多个曲面

使用 MATLAB 的 mesh() 函数的优点

使用 MATLAB 的 mesh() 函数的缺点

相关帖子

MATLAB - 图像处理中的巴特沃斯低通滤波器

掌握 MATLAB 中的表格

MATLAB 中的线性间隔向量函数

MATLAB 和 Scilab 的总体差异

非线性动力学

MATLAB 中高效内存分配的重要性

从 Matlab 中的图像中提取位平面

Z 变换 MATLAB

MATLAB - 电子表格

MATLAB 中的函数参数验证

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器