高斯消元法和高斯-约旦消元法

有两种解决线性方程组的方法

• 高斯消元法
• 高斯-约旦消元法

它们都基于一个观察结果，即如果方程组具有相同的解集，那么它们是等价的，并且对矩阵的行执行简单的运算，称为基本行运算或(EROs)。

有 3 个 ERO

1. 缩放： 将一行乘以一个标量（意味着将该行中的每个元素乘以相同的标量）。这被写成 sr_i⟶r_i，表示行 i 通过乘以标量 s 进行修改。
2. 交换： 交换两行的位置。这被写成 r_i⟵⟶r_j，表示交换了行 i 和 j。
3. 替换： 用该行加上或减去一个标量乘以另一行的结果替换一行中的所有元素。这被写成 r_i± sr_j⟶r_i。

示例

交换行的例子是 r₁⟵⟶r₃。

现在，从这个矩阵开始，缩放的例子是：2r₂⟶r₂，这描述了第 2 行的所有项目都乘以 2。

现在，从这个矩阵开始，替换的例子是：r₃-2r₂⟶r₃。逐个元素地，第 3 行被第 3 行中的元素减去 2 * 第 2 行中的对应项目替换。这会产生

高斯法和高斯-约旦法都从方程组的矩阵形式 Ax = b 开始，然后用列向量 b 扩充系数矩阵 A。

高斯消元法

高斯消元法是一种求解矩阵方程 Ax=b 求解 x 的方法。

这个过程是

1. 它首先用列向量 b 扩充矩阵 A。
2. 它执行 ERO 以将此增广矩阵转换为上三角形式。
3. 它使用回代来求解 x 中的未知数。

示例

使用 2 x 2 系统，增广矩阵将是

然后，使用 ERO 将增广矩阵转换为上三角形式

所以，这只是用 0 替换 a₂₁。 这里，撇号表示值已更改。

将其放回方程形式会产生

对每一行执行此矩阵乘法会产生

所以，解是

类似地，对于 3x3 系统，增广矩阵简化为上三角形式

这将通过首先在 a₂₁ 位置得到 a₀，然后得到 a₃₁，最后得到 a₃₂ 有序地完成。

然后，解将是

考虑以下 2x2 方程组

x₁+2x₂=2
2x₁+2x₂=6

作为矩阵方程 Ax = b，这是

第一个过程是用 b 扩充系数矩阵 A 以获得增广矩阵 [A| b]

对于前向消元，我们需要在 a₂₁ 位置得到 a₀。为了实现这一点，我们可以通过从矩阵的第二行中减去 2 * 第一行来改变它。

我们编写此 ERO 的方式是

现在，将其放回矩阵方程形式

说第二个方程现在是 -2x₂= 2，所以 x₂ = -1。代入第一个方程

x₁+2(-1)=2
x₁=4。

这称为回代。

高斯-约旦消元法

高斯-约旦消元法从高斯消元法开始类似的技术，但是，它使用回代，而是继续消元。

高斯-约旦法包括

• 创建增广矩阵 [A b]
• 通过实施 ERO 进行前向消元以获得上三角形式
• 后向删除到对角线过程，产生解

示例

使用 2x 2 系统，增广矩阵将是

使用 3x 3 系统，增广矩阵将是

注意：结果对角线形式不包括最右边的列。

例如，对于 2x2 系统，前向消元产生了矩阵

现在，为了继续后向消元，我们想要 a₀ 在 a₁₂ 位置。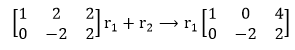

所以，解是

这是一个 3x3 系统的例子

以矩阵形式，增广矩阵 [A|b] 是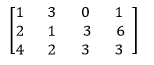

前向替换（通过首先在 a₂₁ 位置得到 a₀，然后 a₃₁，最后 a₃₂，有序完成）

对于高斯技术，这之后是回代

对于高斯-约旦技术，这被后向消元代替

这是一个使用 MATLAB 执行这些替换的例子