反射与对称 6年级笔记

反思和对称是两个在许多方面都联系在一起的概念。反思和对称之间的关系可以在自然界发生的各种活动中观察到。例如，我们可以看到城市湖泊中摩天大楼的倒影，水体中树木或山脉的影像，或者蝴蝶翅膀的对称性等等。反思和对称的概念并不新鲜，它已经存在了几个世纪。例如，在中世纪的城堡中，非常普遍地使用玻璃碎片来创造壮观的对称设计，这增强了场所的整体美感。这种设计理念在今天的精品店和宗教建筑的装饰中仍然被使用。

在数学中，尤其是在几何学中，反思和对称的概念在描述许多高级概念中起着重要作用。此外，对于日常应用的理解这两个概念也是必要的。

什么是反思？

反思可以定义为光线在撞击任何物体后返回的性质。当光线照射到水、玻璃、抛光金属等光亮表面时，它会以特定角度返回并反射。由于光线的这种性质，可以在水体和镜子中看到影像。

反思的类型

反思主要有两种类型，例如

• 规律反射： 当光线从光滑表面反射时，称为规律反射。它也称为“镜面反射”。在这种反射类型中，光线只向一个方向反射。
• 漫反射： 当光线从粗糙表面反射时，称为漫反射。在这种反射类型中，光线向各个方向反射。

什么是对称？

简单地说，对称是指一个物体在被分成两部分后，形状和/或大小完全匹配。比例均匀平衡的物体或形状是称作对称的。某些物体的这种特性通过其外观使事物更加美丽。

考虑一个从一张纸上剪出心形的真实生活场景。为此，我们只需将纸从中对折，在折叠处画半颗心，然后将其剪成半颗心形。然而，当我们展开纸时，我们会得到一个完美而完整的心形。在这种情况下，心的前半部分与后半部分完全匹配。雕刻的心是称作对称的一个例子。

对称的类型

对称主要有四种类型，例如

• 旋转对称： 在旋转对称中，当物体绕其轴（即绕其中心点）旋转时，从所有侧面看起来都相同。当我们在其轴上旋转正方形或圆形时，可以看到旋转对称的例子。旋转过程中，中心点保持固定。
• 反射对称： 顾名思义，这种对称类型涉及反射。当一条线将一个物体分成大小相等的两半时，称为反射对称。它也称为镜面对称或线对称。蝴蝶翅膀通常表现出反射对称。
• 平移对称： 当一个物体从其原始位置在给定方向上移动（或平移）一定距离，并且原始物体和移动的物体仍然完全匹配时，就表示平移对称。砖墙是平移对称的一个常见例子，因为砖块在水平和垂直方向上都以规则的图案重复。
• 滑动反射对称： 滑动反射对称是指两个操作的组合：沿着一条线进行反射，以及沿着同一条线进行平行平移。滑动反射对称的一个例子是沿直线延伸的脚印痕迹。

什么是反射对称？

在各种对称类型中，反射对称在最基础的层面上进行教学，因为它涉及在现实生活中常见的反射。如上所述，反射对称是指一条线将一个物体分成两半，其中一半是另一半的镜像。人脸的左右两侧和蝴蝶两侧的翅膀是一些通常展示反射对称的例子。

让我们关注与反射对称相关的一些基本特征或特性

• 一个物体可能有一条或多条反射对称线，这些线可以朝任何方向。
• 当镜子放置在任何物体中间的线上时，物体的一半会被镜子反射，形成与另一半相同的另一半。
• 放置在中间线旁的镜子通常会将物体分成大小相等的两部分。
• 由线在两侧形成的各个部分以完全相同的距离反射。

反思与对称的应用

在物体的对称线上，图形被反射并在另一侧形成。在这种情况下，原始图形和反射图形是相同的。通常，两侧形成的图形大小相同，并且距离相等。这种类型的反思和对称几乎可以在所有领域或工作领域中看到，无论是艺术、建筑还是设计等。

对称是数学中的一个基本概念，在问题解决技术中起着至关重要的作用。当镜子放置在某些字母的中心时，由于反射对称，可以看到一半字母的反射图像。显示反射对称的一些字母是 A、H、W、M 等。

一种叫做万花筒的仪器，通常是圆柱形或三角形的，由三个或更多镜子组成。该仪器通常用于容纳彩色物体，如珠子或玻璃碎片。当光从一端进入，从另一端观看时，仪器内的镜子充当反射器，提供多条对称线。这种现象通常是由于镜子中的重复反射而发生的。如果图像有一条或多条线，前半部分是另一半的镜像。

对称轴

对称轴是指画在图形或物体上的特定线，它通常将给定的物体/图形完全分成大小相等的两部分。它也称为**对称轴**。由对称轴形成的物体的一半会反射或呈现另一半的镜像。

形状的对称性

在数学中，使用不同的几何形状来教授或理解不同的概念。根据形状的不同，对称轴的数量也不同，并且可以在不同形状中以不同的方式绘制。有些形状可能只有一条对称线，而有些形状可能有多条对称线。

以下是一些具有可能对称轴的常见几何形状，相对于形成的反射

• 正方形： 正方形是二维形状或四边形，有四条边和四个角，所有边长度相等，每个角等于 90 度。正方形可以沿着对角线和垂直及水平的边分成相等的两部分，因此它有四条对称线。

• 长方形： 长方形是二维形状或四边形，有四条边和四个角，其中相对的边平行且相等，每个角等于 90 度。长方形可以沿着宽度和长度分成相等的两部分，从而在其内部创建两条对称线。

• 圆形： 圆形定义为封闭的二维形状，其中曲线上所有点到固定点（称为中心）的距离都相同。圆形可以沿着其直径分成两半。然而，一个圆可以有无限数量的直径。因此，可以说一个圆有无限数量的对称线。

• 三角形： 三角形定义为二维几何形状或三边形，其中三个角包含在三条边内。根据三角形的类型，三角形可以有 1、2 或更多条对称线。有些三角形可能没有任何对称线。此外，等边三角形有三条对称线。

已解决的问题

问题 1：为给定的形状画出对称轴

解答： 对于给定的图形（a）、（b）和（c），图形（a）没有对称线，而对于图形（b），有一条对称线，第三个图形（c）有两条对称线，如下所示

问题 2：以下图形的反射对称是什么样的？

解答： 本题给出的图形是星星、月亮和太阳，这三个图形的反射将与原图形看起来一样。请参阅以下图形中的这些图形的反射对称。

问题 3：画一个没有任何对称性的任意随机形状。

解答： 以下形状没有对称性

问题 4：以下图像是否显示关于 x 轴的任何对称性？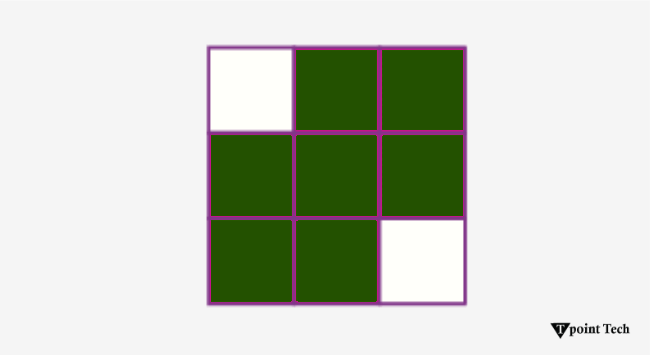

解答： 本题所示图像沿 x 轴没有对称性。然而，它显示了对角线对称。

问题 5：在正方形、六边形和三角形的形状中显示平移对称。

解答： 在以下图形中，正方形从第一象限平移到第三象限，六边形从第二象限平移到第三象限，三角形从第二象限平移到第四象限。

常见问题解答

1. 什么是反思？举例简要说明。

反思是指光线在撞击任何光亮表面后返回的现象或性质。一些例子包括抛光金属表面的光线反射、镜子中人的反射、静止水中的山脉反射等。

2. 什么是对称？举一个真实的对称例子。

对称被定义为一个物体在被分成两部分后，形状和/或大小完全匹配。从雪花到向日葵，从海星到鲨鱼，自然界的许多场景中都可以发现对称。

3. 有哪些值得注意的反思和对称类型？

反思有两种类型，即规律反射和漫反射。此外，不同类型的对称包括旋转对称、反射对称、平移对称和滑动反射对称。

4. 你能判断一个平行四边形是否对称吗？

一般来说，平行四边形的形状看起来可能像它可能是对称的。然而，它在任何反射轴上都不是对称的。

5. 长方形、圆形和正方形有多少条对称线？

长方形有两条对称线，因为我们可以沿着其宽度或长度将其分成相等的两部分。圆形可以有无限数量的对称线，因为它可以沿着任何直径分成相等的两部分。正方形有四条对称线，因为我们可以沿着其对角线以及沿其边（垂直和水平）将其分成相等的两部分。