整数 6年级笔记

整数是包含正（+）和负（-）整数以及零的一组数字。 “整数”一词源自拉丁语，意为“完整”或“完全”。这意味着整数是没有分数或小数点的数字。

整数：快速概述

整数由正整数及其负数组成，例如2及其负数是-2。 换句话说，当我们向整数集添加负数时，我们就得到了完整的整数集。

整数的历史

如前所述，“整数”一词源于拉丁语“integer”，意为“完整”或“未触及”，由in（不）和tangere（触摸）构成。

最初，整数指的是正整数，与自然数同义。随着时间的推移，概念扩展到包括负数，认识到它们的数学价值。莱昂哈德·欧拉（Leonhard Euler）在1765年将整数定义为包含正数和负数。 “整数集”一词在19世纪末随着格奥尔格·康托尔（Georg Cantor）集合论的发展而出现。符号ℤ源自德语Zahlen（数字），由大卫·希尔伯特（David Hilbert）推广，并于1947年首次出现在教科书中。 到了20世纪50年代，“整数”一词开始排除负整数，而“整数”则涵盖正数和负数，这种区别一直延续至今。

整数的定义

整数是任何不含分数或小数的整数。它可以是正数（+），负数（-）或零。 整数的一些例子包括-4、0、2、15、45和7895。整数集通常用符号Z表示，包括以下内容

• 正整数：大于零的数字，如1、2、3等。
• 负整数：小于零的数字，如-1、-2、-3等。
• 零：一个中性整数。它不属于正数或负数类别。

整数集表示如下

Z = {... -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...}

整数符号

整数集通过符号“ℤ”表示。这个符号源自德语单词“Zahlen”，意为“数字”。 在数学中，此符号常用于表示所指的值为整数。

整数的种类

整数通常分为三种不同的类型

1. 零

零是一个独特的整数，在数轴上占据中性位置。它不被认为是正数或负数。 在数学中，零扮演加法单位元的作用，这意味着将零加到任何数字都不会改变其值。它被表示为0。

示例

7 + 0 = 7

−4 + 0 = −4

2. 正整数

正整数包括大于零的整数。 这些数字通常出现在数轴上零的右侧。它们可以带“+”号或不带任何符号。

例子包括

+4, 9, +12, 76

这些数字用于表示收益、海拔或高于基线的数量。

3. 负整数

负整数是数值小于零的整数。 它们总是用负号表示，并且位于数轴上零的左侧。这些数字通常表示损失/减少、温度下降或低于海平面的测量值。

例子包括

−3, −11, −25, −100

数轴上的整数

数轴是一条直线、水平的线，用于按顺序显示数字。数字以相等间隔放置在向两个方向无限延伸的线上。整数可以很容易地显示在这条线上。

数轴上的整数可视化

使用数轴有助于理解和比较整数。以下是一些重要的注意事项

• 位于数轴右侧的数字大于左侧的数字。
• 正整数在0（零）的右侧。
• 负整数在0（零）的左侧。
• 零位于中心，因为它是一个中性/特殊整数（既不是正数也不是负数）。

整数运算

我们可以对整数执行四种基本数学运算

1. 整数加法
2. 整数减法
3. 整数乘法
4. 整数除法

重要提示

• 如果数字前面没有符号，则假定为正数。例如，7等同于+7。
• 整数的绝对值始终是正数。
• 示例：|−4| = 4 且 |4| = 4

1. 整数加法

整数加法是指将两个或多个整数（可以是正数或负数）组合起来。结果取决于所涉及数字的符号。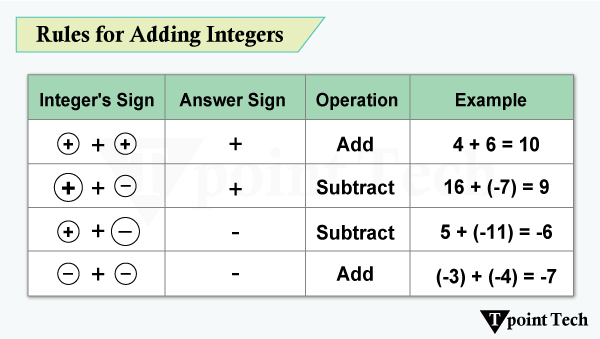

整数加法规则

以下是您需要遵循的基本规则

• 同号：将绝对值相加，并用相同的符号标记答案。
• 异号：从较大的绝对值中减去较小的绝对值。答案的符号将与具有较大绝对值的数字的符号相同。

示例1：计算 (-3) + (-6)

这里，两个整数都是负数。因此，我们加上它们的绝对值

3 + 6 = 9

由于两个数字都是负数，结果也将是负数。

答案 -9

示例2：计算 4 + (-7)

我们首先计算7和4之间的差，即3。

由于7较大且带有负号，因此答案为负数。

答案 -3

数轴上的加法

也可以使用数轴进行整数加法

• 从第一个数字开始。
• 如果涉及正数，则向右移动。
• 如果涉及负数，则向左移动/偏移。

例如：在数轴上求6 + (-9)的和

从6开始，然后向左移动9步，因为它涉及加一个负数。

您将落在-3上。

答案 6 + (-9) = -3

2. 整数减法

整数减法涉及找到两个值之间的差。为了简化过程，我们将减法问题转换为加法问题。

整数减法规则

• 将减法转换为加法。
• 反转第二个数字（减数）的符号。
• 遵循加法规则。

示例1：计算 9 - 13

首先，让我们将其更改为：9 + (-13)

现在减去绝对值：13 - 9 = 4

由于13较大且带有负号，因此结果为负数。

答案 -4

示例2：计算 (-4) - (-7)

解决方案

首先，让我们将减法转换为加法

(-4) + (+7)

现在减去 7 - 4 = 3

由于7较大且为正数，因此结果为正数。

所以，结果是 3

3. 整数乘法

当我们乘以两个整数时，结果可能是正数或负数，这取决于所涉及数字的符号。 有一些明确的规则可以帮助我们确定乘积的正确符号。

整数乘法规则

• 如果两个整数都是正数，结果将始终是正数。
• 示例：4 × 5 = 20
• 如果将正数乘以负数，结果将是负数。
• 示例：7 × (–2) = –14
• 如果负数乘以正数，结果将是负数。
• 示例：(–6) × 3 = –18
• 如果将两个负数相乘，结果将是正数。
• 示例：(–8) × (–2) = 16

4. 整数除法

整数除法涉及将给定数字分成相等的部分。 就像乘法一样，除法也遵循某些规则，并取决于被除数和除数的符号。结果的符号取决于所涉及的整数是正数还是负数。

整数除法规则

要除以两个整数，我们遵循特定的符号规则

• 当正数除以另一个正数时，结果始终为正数。示例：20 ÷ 5 = 4
• 如果正数除以负数，答案将为负数。示例：16 ÷ (–4) = –4
• 如果负数除以正数，结果也将为负数。示例：(–18) ÷ 3 = –6
• 如果两个数字都带有负号，则答案将为正数。示例：(–24) ÷ (–6) = 4

除以 (–30) ÷ 6

• 一个数字是负数，另一个是正数。
• 除以绝对值：30 ÷ 6 = 5
• 由于符号不同，最终答案是负数。

所以，答案是 –5

整数的关键特征

整数遵循几个重要的数学规则或性质。这些规则有助于执行加、减、乘、除等运算。

与整数相关的基本性质包括

1. 封闭性
2. 结合律
3. 交换律
4. 分配律
5. 加法逆性质
6. 乘法逆性质
7. 恒等性质

1. 封闭性

这个性质表明，如果我们对两个整数进行运算，结果也将是一个整数。 换句话说，整数在算术运算（加、减、乘）下是封闭的。然而，除法可能并不总是得到整数的结果。

假设a和b是整数。那么

a + b 也将是一个整数

a − b 仍然是一个整数

a × b 得到另一个整数

a ÷ b 可能不总是整数（例如，5 ÷ 2 = 2.5，这不是整数）

2. 结合律

根据结合律，我们在加法或乘法时对数字进行分组的方式不会影响最终结果。 此规则仅适用于加法和乘法，不适用于减法或除法。

对于任意三个整数a、b和c

(a + b) + c = a + (b + c)

(a × b) × c = a × (b × c)

3. 交换律

交换律解释了在加法或乘法时交换两个数字的顺序永远不会改变结果。 此规则仅适用于加法和乘法，不适用于减法或除法。

对于任意整数a和b

• a + b = b + a
• a × b = b × a

4. 分配律

这个性质将乘法和加法（或减法）联系起来。 根据此性质，将一个数字乘以两个数字的和（总和）或差，与将该数字分别乘以每个加数或减数，然后对结果进行加法或减法，得到相同的结果。

对于任意整数a、b和c

• a × (b + c) = (a × b) + (a × c)
• a × (b − c) = (a × b) − (a × c)

5. 加法逆性质

每个整数都有一个相反数，当它们相加时，结果为零。这个相反数称为加法逆元。

对于任意整数a

a + (−a) = 0

示例：7 + (−7) = 0

6. 乘法逆性质

此性质指出，如果您将任何数字乘以其倒数（或乘法逆元），答案始终是1。 然而，这仅适用于非零数字，因为零没有倒数。

对于任意整数a（除了0）

a × (1/a) = 1

示例：4 × (1/4) = 1

7. 恒等性质

此性质突出了一些特殊数字，当它们用于加法或乘法时不会改变其他数字。

加法恒等元是0，因为将零加到任何数字都不会改变其值

a + 0 = a

乘法恒等元是1，因为将任何数字乘以1会使其保持不变

a × 1 = a

整数的基本事实

个人首次接触整数的场合之一是在早期教育中，当他们开始数数时。当他们在心理数轴上重复数值（甚至用手指计数）时，他们开始认识一种被称为连续整数的模式。有了这种基本理解，他们可以进而进行更复杂的整数运算，例如除法和乘法。

常见问题

以下是关于该主题的一些快速常见问题解答。

问题1：说明整数的目的

答：整数在数学和计算机编程中都扮演着至关重要的角色。 在编码中，整数广泛用于计数或增加值，例如在“for循环”或“while循环”中。它们对于识别数组或列表中元素的位置也至关重要。由于数学围绕数字展开，整数帮助我们有效地进行各种计算和逻辑运算。

问题2：列出关于整数的关键事实。

答：整数是可以是正数、负数或零的整数，但它们不包括分数或小数。 所有基本的算术运算——例如加、减、乘、除——都可以应用于整数。整数的一些例子是：1、2、5、8、-9、-12等。整数集通常用“Z”表示。

问题3：最小的整数是哪个？

答：0 / 零是最小的整数。

问题4：整数可以用于表示财务中的借方和贷方吗？

答：在财务上下文中，整数有助于跟踪货币交易。正整数表示资金流入，例如收入或存款，而负整数表示资金流出，例如支出、债务或损失。

例如

如果您向储蓄账户存入2,000卢比，可以表示为+2000，这意味着您有贷方或收益。

如果您向朋友借了750卢比，则表示为-750，表明您有债务。

这种整数的使用有助于清晰地显示财务状况并有效地管理账户。

问题5：小数和分数是整数家族的一部分吗？

答：不，小数和分数不属于整数集或整数家族。整数仅限于整数，包括正值和负值，以及零。例如，-4、0和7等数字是整数，但3.5或½不是。

问题6：整数如何帮助解释温度变化？

答：整数有助于显示温度如何上升或下降。正整数表示增加，而负整数表示减少。

例如

• 如果温度升高6°C，则记作+6°C。
• 如果温度下降4°C，则记作–4°C。

这样，我们就能轻松理解温度波动。

问题7：术语“连续整数”是什么意思？

答：连续整数是按顺序出现的数字（每个数字直接跟在前面一个之后），每个数字都增加1。

例如，10、11和12或–2、–1和0等数字是连续整数的例子，因为每个数字都比前一个数字大一。

问题8：整数是整数的一种吗？

答：是的，整数是整数的一种。它们由正整数和零组成，但不包括任何负整数。 本质上，虽然每个整数都是一个整数，但每个整数不都是一个整数。 例如，0、1、2、3等数字既是整数又是整数，而-1、-2、-3等数字是整数但不是整数。