变量在常用规则中的应用 6年级笔记

代数是数学的一个分支，专注于包含变量和常量的表达式和方程。在代数中，变量是方程中未知或未知的值。变量与常量的不同之处在于它们的值不是固定的，并且可以改变。变量在数学的各个领域有不同的用途。

它们在代数规则中很有用，例如在几何中计算周长和面积，以及应用算术定律，如交换律、结合律和分配律。变量对于形成和概括公式、方程和恒等式至关重要。

变量：快速概览

变量是指表示未知值的符号。在数学中，它帮助我们解决某些值未知的问题。在代数中，变量用英文字母表示，如 x、y 和 z。

其他例子包括

• t 代表时间
• r 代表半径
• s 代表弧长
• a、b、c 代表方程中的未知数

这些符号代表我们不知道但需要找到的数字。

代数表达式中的变量

示例

考虑方程3x + 2 = 11。

要确定 x 的值，必须解方程。

3x = 11 - 2 → 3x = 9 → x = 3

在这里，x 是通过求解找到其值的变量。

变量在统计学中的应用

在统计学中，变量一词也有使用，但方式略有不同。这里的变量是指可测量的项目或数量。

例如，在调查或研究中，变量可以是

• 年龄
• 性别 (Gender)
• 收入
• 收入

这些值可以因人而异，用于数据分析。

在通用规则中使用变量

1. 几何规则

变量在几何学中起着重要作用，尤其是在计算形状的面积和周长时。除了这些基本用途外，变量还有助于表达其他几种几何规则。

以下是一些例子

圆的直径可以用其半径表示。如果 d 代表直径，r 代表半径，则关系为

d = 2r

为了找出从多边形的一个顶点可以画出多少条对角线，我们使用变量 n 来表示边的数量。公式变为

n − 3

多边形内角和也基于边的数量。假设多边形有“n”条边，则内角和可以表示为：(n − 2) × 180°

A. 在求周长中使用变量

平面图形的周长是指其形状的完整测量值。通过将各个图形所有边的长度相加来计算。

在此过程中，使用变量来表示边的长度。通过使用这个变量，我们可以写出一个计算周长的通用公式。

• 三角形周长

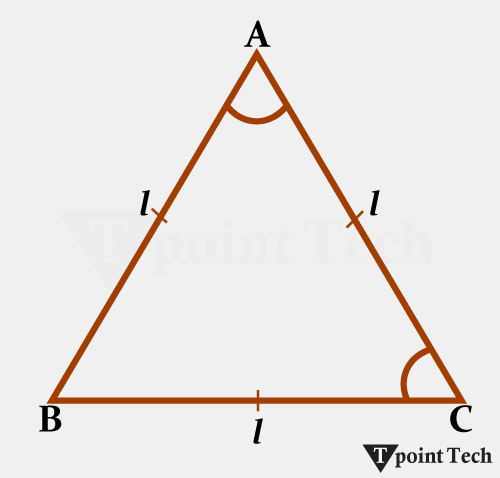在等边三角形中，所有 3 条边的测量值（长度）都相等。如果边用 l 表示，则周长为 3 × l。

• 五边形周长

对于正五边形，所有五条边都相等，每条边用 l 表示，则周长为 5 × l。

• 正方形的周长

正方形有 4 条边。所有边的长度都相等。

因此，正方形的周长 = 所有边之和 = 4 × 边长

如果正方形的一条边的长度是 l，则周长是

周长 = 4 × l = 4l

这条规则使用变量 l 来使其易于记忆。

如果我们使用p表示周长，则

p = 4l

• 矩形的周长

矩形由 4 条边组成。相对边总是相等的。

假设a是长度，b是宽度。

因此，相同周长将是

= a + b + a + b = 2a + 2b

因此，规则是

周长 = 2a + 2b 或 2 (a + b)

如果我们使用 p 表示周长，则变为

p = 2a + 2b

在这里，长度(a) 和宽度(b) 都是未知的，因此它们可以是任何值，并且彼此不相关。

这表明变量如何帮助我们编写和使用通用公式来计算不同形状的周长。

B. 使用变量计算面积

面积是形状内部覆盖的空间。每种形状都有其自己的面积计算公式，我们使用变量来表示这些公式中的边长和尺寸。

在直角三角形中，如果底是 b，高是 h，则面积由公式给出：(1/2) × b × h。

对于等边三角形，所有边都相同并用 a 表示，则面积公式变为 (√3 / 4) × a²。

在正方形中，由于所有边都相等并用 a 表示，则面积变为 a × a 或简称为 a²。

对于矩形，长度为 l，宽度为 b，则面积表示为 l × b。

因此，使用变量可以让我们轻松地为具有给定边长的任何形状编写和使用面积公式。

2. 在数型中使用变量

变量也用于以通用形式表示数型。这包括查找后继数、前驱数、平方、立方、偶数和奇数等模式。

• 要找到自然数的后继数，我们加 1。所以，如果数字是 n，则后继数是 n + 1。
• 要找到前驱数，我们减 1。这意味着 n 的前驱数是 n - 1。
• 一个数“n”的平方是通过将该数乘以自身来计算的，得到 n²。
• 数 n 的立方表示为 n³，意味着 n × n × n。
• 偶数可以写成 2n，其中“n”是整数。
• 奇数写成 2n + 1，其中 n 是整数。

这些规则帮助我们使用变量来理解和创建不同类型的数型。这些模式也适用于其他类型的数字，如整数和有理数，而不仅仅是自然数。

3. 算术规则

A. 加法交换律

这条规则说明改变数字的顺序不会改变它们的和。

例如，a 和 b 是两个数字。那么

a + b = b + a

假设

如果a = 6，b = 9，则 6 + 9 = 9 + 6 = 15

B. 乘法交换律

这条规则说明改变数字的顺序不会改变乘法的结果。

例如，a 和 b 是两个数字。那么

a × b = b × a

例如

如果a = 4，b = 5，则 4 × 5 = 5 × 4 = 20

C. 乘法对加法的分配律

这条规则意味着如果你将一个数乘以一个和，它就等于将该数分别乘以和的每个部分，然后将结果相加。

例如，a、b 和 c 是数字。那么

a × (b + c) = a × b + a × c

示例

如果a = 6, b = 20，和c = 5，

那么：6 × (20 + 5) = 6 × 20 + 6 × 5 = 120 + 30 = 150

D. 加法结合律

让我们取任意三个数字，比如 a、b 和 c。根据加法结合律：

(a + b) + c = a + (b + c)

这表明在相加时分组数字的方式不会改变最终结果。可以按任何顺序进行分组。

E. 乘法结合律

现在，让我们再次考虑三个数字 — a、b 和 c。根据乘法结合律：

(a × b) × c = a × (b × c)

这告诉我们，在乘以三个数字时，分组方式不会影响结果。无论如何分组，结果都保持不变。

变量在代数中的使用方法

在代数中，变量是指代表未知数的符号（如 a、b、c 或 x、y、z）。代数是数学的一个部分，我们在其中使用这些变量来处理表达式和方程。

以下是变量在代数中的一些常见用法

1. 编写表达式和方程

变量有助于形成数学表达式和方程。

示例：x + 5 = 10 是一个方程，其中 x 是未知值。

2. 表示多项式形式和标准方程

变量用于编写多项式和标准方程。

示例：ax² + bx + c = 0 是用变量编写的二次方程。

3. 表示算术和几何序列

在序列和模式中，变量有助于泛化项。

示例：算术序列如 a, a + d, a + 2d, ... 使用变量来显示模式。

4. 创建和表示恒等式

变量也用于形成代数恒等式。

示例：像 (a + b)² = a² + 2ab + b² 这样的恒等式使用变量来对所有值都成立。

结论

变量是用来表示未知数字或数量的符号。它们通常用英文字母表示，如 x、y 或 z。变量在数学的各个领域都有使用，包括算术、代数和几何。

在几何学中，变量有助于编写形状（如矩形和正方形）的周长和面积公式。在算术中，它们用于解释关键规则，如数字在加法和乘法等运算中的交换律、结合律和分配律。

在代数中，变量对于形成方程、表达式和恒等式至关重要。它们在描述模式和数学序列（如算术和几何级数）中至关重要。变量允许我们创建适用于所有数字的通用规则。

常见问题解答 (FAQs)

学生们经常对变量在通用数学规则中的使用方式有很多疑问。以下是一些最常见的问题及其答案。

Q1. 变量在日常生活中是如何利用的？

在现实情况中，表达式中的变量用于表示未知量，这些量可能会发生变化。要为这种情况写一个变量表达式，首先要识别未知量并为其分配一个变量。

Q2. 变量一词在研究中意味着什么？

在研究中，变量可以是正在测量或观察的任何对象、人、地点、事件或思想。

Q3. 为什么变量在数学中很重要？

变量有助于以简单的方式表达数学思想。例如，方程x² + 2x = 6比说“某个数字乘以自身加上该数字的两倍等于六”更容易理解。变量还有助于扩展数学思想以涵盖所有可能的值。

Q4. 使用变量有什么优点？

变量很重要，因为它们有助于我们在研究中学习和理解数据。无论是在实验还是调查中，研究人员都使用变量来收集、测量和分析信息。这有助于发现不同数据集之间的关系。

Q5. 变量的主要特征是什么？

变量是指任何可以测量或计数的東西。它可以代表数据项，如年龄、性别、收入、支出、成绩、眼睛颜色、出生地或车辆类型。变量可能因案例而异，并且对于数据分析至关重要。

Q6. 举例说明在正六边形周长中使用变量。

六边形有六条相等的边。假设每条边的长度用变量 'l' 表示。

因此，在这种情况下，正六边形的周长是

P = l + l + l + l + l + l

这简化为：

P = 6l

在这里，l 是一个变量，代表边的长度，它可以是任何数值。

Q7. 陈述在几何中使用变量的标准规则。

在几何学研究中，变量通常用于写下不同形状周长的公式。例如，对于正方形或矩形，变量代表边的长度或其他测量值，以制作适用于任何值的通用公式。