矩阵定义

矩阵是数字、符号或表达式的矩形数组，按行和列排列。矩阵在数学、工程和科学中被广泛用于表示数据、执行计算和模拟现实世界问题。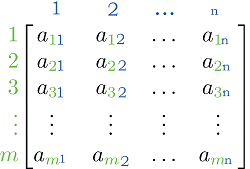

关于矩阵

矩阵通常用大写字母表示，例如 A、B 或 C。矩阵中的元素用带有下标的小写字母表示，例如 aij，其中 i 表示行，j 表示列。

矩阵的性质

矩阵的一个重要性质是它们的大小，它由行数和列数定义。具有 m 行 n 列的矩阵称为 mxn 矩阵。如果矩阵具有相同数量的行和列，则称为方阵。

只要要相加或相减的矩阵大小相同，就可以逐个元素地相加或相减矩阵。换句话说，要对两个矩阵进行相加或相减，只需将对应位置的元素相加或相减即可。

只有当第一个矩阵的列数等于第二个矩阵的行数时，才能定义两个矩阵的乘积。在这种情况下，两个矩阵的乘积是一个新矩阵，其元素是对应行和列的元素乘积之和。

矩阵的类型

矩阵的一个重要类型是单位矩阵，它是一个方阵，主对角线上的元素为 1，其余元素为 0。单位矩阵通常用字母 I 表示，它的性质是，如果它与任何其他矩阵相乘，结果就是原始矩阵。

矩阵的另一种重要类型是对角矩阵，它也是一个方阵，主对角线以外的元素为零。

矩阵的变换

矩阵可以通过各种运算进行变换，例如转置、求逆和对角化。矩阵的转置是一个新矩阵，通过将原始矩阵绕其主对角线进行反射而形成。换句话说，原始矩阵的行变成转置矩阵的列，反之亦然。

矩阵的求逆

求逆是寻找一个矩阵的过程，该矩阵与原始矩阵相乘得到单位矩阵。换句话说，如果 A 是一个矩阵，A^(-1) 是它的逆，那么 A * A^(-1) = A^(-1) * A = I。并非所有矩阵都有逆，但如果一个矩阵确实有逆，则它是唯一的。

对角化

对角化是寻找一个与原始矩阵相似的对角矩阵的过程。这意味着存在一个可逆矩阵 P，使得 P^(-1) * A * P = D，其中 D 是一个对角矩阵。对角化可能很有用，因为它可以简化特征值和特征向量的计算，而特征值和特征向量在数学、科学和工程的许多领域中起着至关重要的作用。

特征值和特征向量是与矩阵相关的特殊标量和向量。矩阵 A 的特征值是一个标量 λ，使得 Av = λv，其中 v 是一个非零向量，称为特征向量。矩阵的特征向量和特征值可用于研究线性变换的性质并求解线性方程组。

矩阵也用于表示线性代数中的线性变换。线性变换是一种将向量映射到向量的函数，它保留了向量加法和标量乘法的性质。线性变换的矩阵表示使我们能够高效且有效地执行变换。

矩阵的应用

此外，矩阵在各种领域都有许多应用。在计算机图形学中，矩阵用于表示旋转、平移和缩放等变换。在经济学中，矩阵用于模拟线性方程组，这些方程组表示变量之间的关系，例如供求关系。在物理学中，矩阵用于表示物理量，例如位置和动量，并用于描述物理系统随时间演化。

在统计学中，矩阵用于表示数据集，其中每一行代表一个观测值，每一列代表一个变量。主成分分析和奇异值分解技术基于矩阵，并广泛用于数据分析和数据压缩。

在控制系统中，矩阵用于模拟动态系统，例如机械系统、电路和控制系统。动态系统的状态空间表示是一组线性微分方程，它描述了系统随时间的变化，而矩阵用于表示这些方程的系数。

矩阵在求解线性方程组中也起着至关重要的作用。高斯消元法和 LU 分解是两种基于矩阵的求解线性方程组的方法，它们在工程和科学中得到了广泛应用。矩阵的行列式是一个标量，它提供了有关矩阵可逆性的信息，并用于计算矩阵的逆。

结论

总之，矩阵是数学中的基本工具，它们在科学、工程和技术领域具有广泛的应用。它们用于表示数据、执行计算和模拟现实世界问题，其通用性和强大功能使其成为从事这些领域工作的任何人的必备工具。