自然数

定义

自然数是我们用来计算物体或事物的数字。换句话说，自然数是所有整数的集合，但不包括零。它是实数的一部分。

它只包含正整数。请记住，0、分数、小数和负数都不是自然数。自然数从1开始，一直到无穷大。例如，1、2、3、4、5、6，等等。

自然数包含所有整数，但不包括零。这意味着所有自然数都是整数，但并非所有整数都是自然数，因为整数也包括0。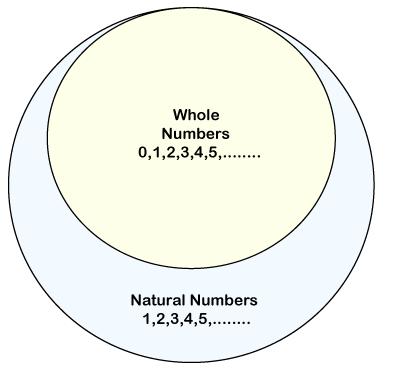

前50个自然数是

自然数的符号

自然数集用字母N表示。

自然数集

自然数集是一个无限集。我们可以用以下三种形式表示自然数集：

• 叙述： N=所有自然数的集合
• 枚举法： N={1,2,3,4,5,6,7,8,9,……}
• 描述法： N={x: x是大于等于1的整数}

关于自然数的趣事

• 它大于零。
• 最小的自然数是1。
• 最大的自然数无法获得。
• 所有自然数都是整数，但反之则不然。
• 如果 x 是一个自然数，那么 x 的后继数是x+1。
• 如果 x 是一个自然数，那么 x 的前驱数是x-1。

自然数的性质

自然数有四种主要性质：

• 封闭性
• 交换律
• 结合律
• 分配律

封闭性

自然数在加法和乘法运算下满足封闭性。这意味着当我们对两个或多个自然数进行加法或乘法运算时，结果总是自然数。

假设 a、b 是两个自然数，c 是结果，那么：

例如，9+5=14，12+3=15等，结果14和15也是自然数。同样，在乘法中20×3=60，15×5=75等，乘积60和75也是自然数。

在减法和除法中，自然数可能满足也可能不满足封闭性。这意味着当我们对两个或多个自然数进行减法或除法运算时，可能会得到负数结果或小数商。

假设 a、b 是两个自然数，c 是结果，那么：

例如，9-5=4，12-3=9等，结果4和9也是自然数。但当我们计算5-9=-4时，得到的结果不是自然数。

同样，在除法中20÷5=4，15÷5=3等，商4和3也是自然数。但当我们计算3÷2=1.5时，得到的结果不是自然数。

交换律

自然数的加法和乘法运算满足交换律。假设 a 和 b 是两个自然数，那么：

自然数的减法和除法不满足交换律。

结合律

自然数的加法和乘法运算满足结合律。

自然数的减法和除法运算不满足结合律。

分配律

自然数的乘法总是对加法和减法满足分配律。

单位元存在性

如果我们给一个自然数加上0，或者将一个自然数乘以1，我们会得到相同的自然数。假设 a 是一个自然数，那么：

让我们看一些例子。

例1：从以下数字列表中，挑选出自然数和非自然数。

-4,20,,2.67,6,90,100000

解决方案

自然数 20,6,90,100000

非自然数： -4，，2.67

例2：写出前10个自然数。

解决方案

前10个自然数是：1, 2, 3, 4, 5, 6, 7, 8, 9, 10。

例3：写出20到30之间的自然数。

解决方案

20到30之间的自然数是：21, 22, 23, 24, 25, 26, 27, 28, 29, 30

例4：计算前10个自然数的和。

解决方案

前10个自然数是：1, 2, 3, 4, 5, 6, 7, 8, 9, 10

有两种方法可以计算自然数的和：

• 使用加法运算
• 使用公式

使用加法运算

1+2+3+4+5+6+7+8+9+10=55

如果我们要相加的自然数很多，这是一个耗时耗力的过程。所以我们通常不使用它。

使用公式

我们需要计算前10个自然数的和，所以 n = 10。

将 n 的值代入上述公式，我们得到：

前10个自然数的和 (S₁₀)=

因此，前10个自然数的和是55。

例5：计算前45个自然数的和。

解决方案

我们需要计算前45个自然数的和。所以，n = 45。

将 n 的值代入上述公式，我们得到：

因此，前45个自然数的和是1035。