面积与周长

我们都一定听过“几何学”这个词，它是数学的一个分支，研究形状、角度、结构及其测量方法，如面积和周长；除此之外，这个数学分支还关注形状和结构的内在属性及其在平面上的相对配置。几何学包含两个希腊词“Geo”和“Metron”。“Geo”的意思是“地球”。“Metron”的意思是“测量”，由此我们可以看出，几何学是描述形状、物体、行星、角度等的测量（面积和周长）的数学领域。

根据形状的维度，几何学主要分为两类。

1. 二维（2-D）几何学
2. 三维（3-D）几何学

一个基本且最重要的点，在二维几何学和三维几何学中都遵循，那就是几何学中研究的所有形状和结构都由点、射线、线和平面构成，我们研究的所有几何形状都是由相交于某公共点并构成平面上封闭结构的线形成的；因此，每个形状都有确定的面积和周长。

数学是一个庞大的学科，有许多分支，而数学中最基本概念之一就是物体的“面积和周长”。在数学中，面积可以指二维（2-D）表面的度量，而周长可以指该物体（如平面、形状、圆形等）的线条的度量。它们是一个基本概念，在各个领域都有许多实际应用。

我们在小学时就开始接触面积和周长的概念，那时我们使用简单的公式计算正方形和矩形等简单形状和物体的面积和周长。在后来的几年里，我们学习了圆形、三角形和正多边形等更复杂的形状。在数学中，面积通常以平方单位测量，如平方厘米、平方米和平方英尺，而周长以单位测量，如厘米（cm）、米（m）和英尺（ft）。

任何物体的面积都有一些基本性质，即两个不同形状的面积相加；当一个物体或形状由不同类型的形状组成时，这一点非常有用，而对于该物体的周长也适用。例如，L形物体的面积可以通过将其分成两个矩形并相加它们的面积来计算。同样，周长也可以通过简单地将数字相加来计算。同样，复杂多边形的面积也可以通过将其分成小的矩形和三角形，然后相加它们的面积来计算。

面积和周长在现实世界中有许多不同的应用；例如，建筑学利用面积和周长的概念来估算建造结构所需的材料量，并且他们还使用面积和周长来计算建筑物内人员移动所需的空间量。

计算物体面积和周长的方法有很多，取决于其形状和特征；例如，三角形的面积可以通过将三角形的底乘以高然后除以二（2）来计算。三角形的周长可以通过简单地将所有边相加来测量。在本文中，我们将学习许多关于不同形状的面积和周长的知识。

面积与周长的历史

自古以来，“面积和周长”就是人类历史的重要组成部分，因为人类一直对测量和占据周围空间感兴趣。面积的历史可以追溯到古代文明的美索不达米亚、埃及和印度，在那里我们的祖先开发了数学系统来测量土地、建筑物和其他物理空间。

在古印度，面积的概念作为吠陀时期数学传统的一部分得到了发展。我们都知道，地球周长的第一个正确测量是由“阿耶波多”在公元 5 世纪进行的。在“乔提耶”的著名著作《政事论》中，我们了解了当时使用的各种测量单位，如角、由旬和弓。在《政事论》中给出了角、由旬和弓之间的关系，‘角’字面意思是‘手指’，这表明在古印度，人们曾经用身体部位来测量长度和宽度。通过测量“摩亨佐·达罗”的建筑，计算出当时一个角的平均尺寸精确等于 1.6764 厘米。

在美索不达米亚，世界上最早的文明之一，这些民族发展了一种基于人体长度的测量系统，称为肘尺。该系统用于测量长度和面积；在该系统中，一平方肘尺等于一平方英尺的面积。后来的巴比伦人（他们也是美索不达米亚人）开发了一个更适合的测量系统，其中包括面积单位，如阿鲁拉和比尔图，用于测量农田。

在古埃及，面积的概念主要用于测量和测量农田，因为肥沃的土地稀缺。埃及人开发了一种基于肘尺和掌的测量系统，用于测量长度和面积。他们还使用绳子和木桩系统来划定田地和其他土地区域的边界。我们知道，埃及的首都“开罗”以其巨大的金字塔结构而闻名。没有面积和周长知识能建造那些结构吗？答案是否定的。

在中世纪，几何学和数学的研究继续发展；来自伊斯兰学者如花拉子密的杰出贡献，他发展了代数概念，并在三角学方面取得了重要改进（发现）。面积概念在此期间得到了进一步发展，数学家们利用几何学和微积分原理开发了计算复杂形状面积的方法。

在现代，面积概念已成为许多研究领域的核心，包括数学、物理学和工程学。“艾萨克·牛顿”当我们读到这个名字时，我们会想到“万有引力定律”，但您知道吗？数学中的积分概念是由艾萨克·牛顿开发的，积分是求复杂形状物体面积的基本概念。计算机和数字技术的发展为查找和计算不同物体的面积开辟了新途径。它使得面积概念能够以新的和创新的方式得到应用。

今天，面积概念仍然对我们理解周围世界至关重要，从建筑物和城市的大小到生态系统和地球本身的测量。随着我们对宇宙及其复杂性的理解不断增长，面积概念无疑将在帮助我们理解和量化广阔空间和时间方面发挥重要作用。

定义

• 面积

在数学中，特别是在几何学中，面积可以定义为二维形状或表面的度量或范围，简单地说，它是任何物体或事物在表面（2D）上所覆盖的空间。

• 周长

物体的周长可以定义为外部边长之和；简单地说，任何物体的周长等于缠绕或沿着该形状的边追踪的线的长度。

面积的概念与周长密切相关，周长是通过将形状或表面的所有边长相加来计算的。然而，虽然周长只描述了形状或表面的边界长度，但面积描述了该边界所包围的空间量。

测量面积的单位

我们听说过英尺、米和公里是测量单位，但我们有没有想过为什么没有单一的单位系统来测量任何事物的长度？它被称为 SI 系统，其完整形式是“Système International”，也称为国际单位制。它是在 1960 年建立的基础，用于制定世界各地不同事物的标准测量单位。

因此，为了测量长度，我们有米、英尺和公里作为标准单位。一米等于 100 厘米，一公里等于 1000 米，一英尺等于 30.48 厘米。它们有不同的缩写来表示，例如厘米的缩写是 cm，米的缩写是 m，公里的缩写是 km，英尺的缩写是 ft。

• 1 英尺 = 30.48 厘米
• 1 米 = 100 厘米
• 1 公里 = 1000 米

不同形状的面积与周长

有各种公式和方法用于计算不同形状的面积，例如三角形、圆形、矩形和不规则多边形。一般来说，计算形状面积的公式涉及将底或直径乘以高或半径，或者将复杂形状分解成较小且简单的形状或部分，其面积可以轻松计算然后将它们加在一起。同时，任何形状的周长都可以通过简单地将该形状的所有边相加来计算。我们将学习一些基本形状的面积和周长的基本公式。

1. 正方形

在数学中，正方形可以定义为一种封闭的四边形或结构，其四条边长度相等；此外，所有四个角的大小相等，即 90 度或 π/2。正方形有四个顶点，因此有两条对角线，其长度也彼此相等。正方形物体的周长是通过将所有四条边的长度相加得到的。正方形物体的面积是通过边长的平方得到的，而周长是通过边长的四倍得到的。如下图所示。

2. 矩形

在数学中，矩形可以定义为一种封闭的四边形，其相对边长度相等；它也有每个角为 90 度。矩形有四个顶点；因此，两条对角线长度相等。矩形物体的周长是通过将所有四条边的长度相加得到的。矩形物体的面积是通过将矩形的长度和宽度相乘得到的。如下图所示。

3. 三角形

“三角形”这个词可以分解为两部分，“tri”和“angle”，意思是三个角。因此，基于此，三角形可以定义为一种封闭的三边结构或形状，有三个角；它有三个顶点，所以没有对角线。三角形物体的周长是通过将所有三条边的长度相加得到的。三角形物体的面积是通过将底乘以高除以二（2）得到的。如下图所示。

4. 直角三角形

正如我们从它的名字可以看出，直角三角形可以定义为其中一个角为 90 度的三角形。著名的勾股定理是为这种直角三角形而设的。三角形物体的周长是通过将所有三条边的长度相加得到的。三角形物体的面积是通过将底乘以高除以二（2）得到的。如下图所示。

5. 等边三角形

正如我们从等边三角形的名字可以看出，等边三角形可以定义为三条边长度都相等的三角形；因此，等边三角形的所有三个角也相等，即 60 度。三角形物体的周长是通过将所有三条边的长度相加得到的。三角形物体的面积是通过将底乘以高除以二（2）得到的；它也可以通过等边三角形边长的平方乘以 sqrt (3)/4 来确定。如下图所示。

6. 等腰直角三角形

等腰可以分解为两部分，“Iso”和“scale”，意思是相同的边；基于此，等腰直角三角形可以定义为一条三角形有两条边长度相等，且这两条边之间的夹角为 90 度。三角形物体的周长是通过将所有三条边的长度相加得到的。三角形物体的面积是通过将底乘以高除以二（2）得到的。如下图所示。

7. 圆

圆是一种二维形状或表面，没有角也没有顶点，它可以定义为与一个给定点（称为圆心）等距的点形成的路径，该距离称为圆的半径。圆的周长是半径的两倍与 pi（π）的乘积。

圆的面积是 pi（π）与圆半径平方的乘积，圆的周长是 pi（π）与半径乘积的两倍。如下图所示。

8. 菱形

在数学中，菱形可以定义为一种封闭的四边形或形状，其四条边长度相等（与正方形相同），但边之间的角度大小不同。它有四个顶点和两条对角线，长度不同。因此，正方形是菱形的一个特例。菱形的周长是其边长与四的乘积。菱形的面积是两条对角线长度之积除以二。如下图所示。

9. 平行四边形

在数学中，平行四边形可以定义为一种封闭的四边形或形状，其相对边长度相等（与矩形相同），但边之间的角度大小不同。它有四个顶点，因此有两条长度不同的对角线；矩形是平行四边形的一个特例。不平行边的和的两倍给出平行四边形的周长。平行四边形的面积是平行四边形的高与底的乘积。如下图所示。

10. 梯形

在数学中，梯形可以定义为一种封闭的四边形或形状，其中有两条相对的平行边和两条相对的不平行边。它有四个顶点，因此有两条长度不同的对角线。梯形物体的周长是通过将所有四条边的长度相加得到的。梯形的面积是梯形的高乘以平行边之和再除以二（2）。如下图所示。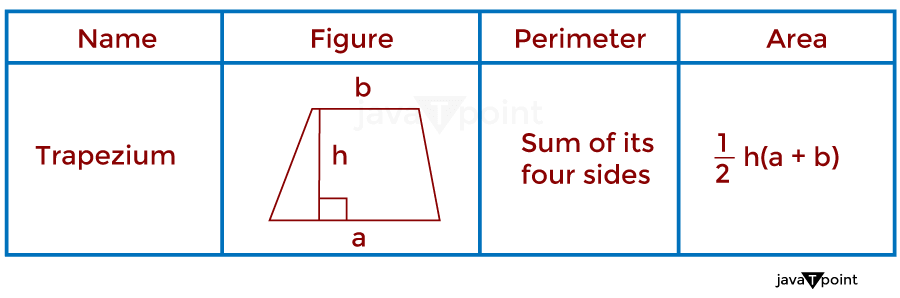

应用

面积和周长的概念，它们测量二维区域或形状的大小，在各种领域都有各种应用。以下是一些例子：

1. 工程学：工程师利用面积和周长的概念设计建筑物、桥梁和道路等结构；他们还利用它来计算管道、电缆和其他部件的横截面积和周长。
2. 数学：面积和周长的概念是几何学和三角学的基石，用于解决涉及三角形、圆形、矩形和多边形等形状的问题；微积分也利用面积的概念来求曲线下的面积。
3. 农业：在农业中，面积和周长的概念用于确定农作物所需的土地量，并计算单位面积的产量。
4. 物理学：面积用于物理学中计算量，例如光束横截面的面积、表面的面积以及电容器板的面积。
5. 地图学：地图代表一个区域，区域的面积是地图制作中的一个重要因素。地图制图师利用面积的概念在地图上以特定的比例准确地描述（绘制）不同区域的大小。
6. 建筑学：建筑师利用面积的概念来设计和规划建筑物的布局，并计算建造所需的材料量。
7. 经济学：面积和周长的概念用于经济学中计算需求曲线或供给曲线下的面积，该面积代表与特定生产水平相关的总收入或总成本。
8. 环境科学：面积的概念用于环境科学中计算栖息地或生态系统的大小，这对于理解生态系统的生物多样性和健康至关重要。

这些只是面积概念在各个领域众多应用中的几个例子。

结论

我们可以说，面积和周长的概念在几何学和各种现实世界的应用中都起着至关重要的作用。面积是指形状所包围的二维表面的范围，而周长代表其边界的总长度；这两种度量对于理解和量化形状和图形的空间特征至关重要。

纵观历史，数学家和科学家们一直在深入研究面积和周长，以揭开自然界的秘密并建造文明；从古代到现代，这些概念被应用于建筑、工程、土地测量等众多领域。它们对于设计建筑物、规划城市和确定建造所需的材料至关重要。此外，面积和周长不仅限于正方形、圆形或三角形等简单形状。数学的进步使得计算复杂和不规则图形的这些度量成为可能，从而使其在计算机图形学、图像处理和地理信息系统等多样化行业中具有应用性。