复数

形如 x^2 + 4 = 2 或 x^2 + 1 = 0 的方程是无解的，因为不存在一个有理数的平方等于 -2 或 -1。欧拉是第一位引入“虚数单位”(iota) 这个术语来表示负数平方根（例如 -1）的数学家。虚数单位进一步演变成了“虚数单位”。数学家利用 i^2 = -1 的性质计算了方程 x^2 + 1 = 0 的解。

复数表示一个数中实部和虚部的组合。

首先，让我们讨论一下实数和虚数是什么。

实数

实数是以分数、整数和无理数形式存在的数字。例如，

虚数

虚数是包含虚数单位(iota)的数。虚数的平方是负数。

例如：

这是因为虚数单位的平方等于 -1。虚数的例子是

因此，复数可以表示为

其中，

a 和 b 是两个实数。

带有虚数单位的项称为数字的虚部。不带虚数单位的项称为数字的实部。没有实部的数称为纯虚数。同样，没有虚部的数称为纯实数。

例如：

复数的视觉表示

让我们从视觉上理解复数。

如图所示，图上的两条轴是实轴和虚轴

复数 z = a + ib 可以表示为

这里，a 和 b 是实轴和虚轴上的数值。

让我们在上面的图上表示一些复数。

1. 3 + 2i

给定复数的坐标是 (3, 2)。这里，数字 3 位于实轴上，数字 2 位于虚轴上，如图所示

2. -2 - 4i

给定复数的坐标是 (-2, -4)。这里，数字 -2 位于实轴上，数字 -4 位于虚轴上，如图所示

数字被分为实数和复数。一个数字包含两个部分，即实部和虚部。实数只包含实部，而复数包含实部和虚部。

虚部的平方是负数，而实部的平方是正数。例如，

我们也可以说负数的平方根是虚数。

虚数(Iota)的幂

在这里，我们将讨论虚数单位 (i) 的正幂和负幂。

i 的正幂

因此，我们可以说

i 的负幂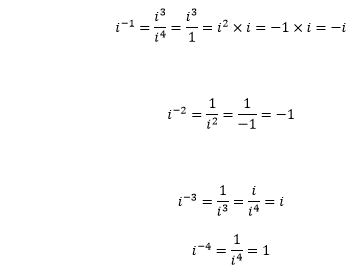

让我们计算虚数的高次幂。

通过以上四个正幂，可以轻松计算出虚数的高次幂。

示例：计算下面给出的虚数幂

(a)=i^-999

(b)=i¹³⁵

解决方案

(a) 我们知道，

i⁴=1

当我们用 4 除以 999 时，余数为 3。

我们可以写成

(b) 当我们用 4 除以 135 时，余数为 3。

我们可以写成

复数相等

设两个复数为 z1 和 z2。

如果 z1 = a1 + ib1

z2 = a2 +ib2

当且仅当 a1 = a2 且 b1 = b2 时，上述复数相等。

这意味着 z1 的实部 = z2 的实部，z1 的虚部 = z2 的虚部。

让我们通过几个例子来理解。

示例 1：如果 z1 = 4 - iy 且 z2 = x + 5i 相等，则求 x 和 y 的值。

已知：z1 = z2。

4 - iy = x + 5i

我们知道，Re (z1) = Re (z2)

比较后，我们得到，

x = 4

同样，令 Im (z1) = Im (z2)

我们得到，

y = -5 或 -y = 5

示例 2：求 a 和 b 的值，如果

(a + b) - i (3a + 2b) = 5 + 2i

令实部和虚部相等，我们得到

a + b = 5 且 3a + 2b = 2

求解以上两个方程，我们得到

a = -12

b = 17

复数加法

设两个复数为 z1 和 z2，其中

z1 = a1 + ib1

z2 = a2 +ib2

两个复数 z1 和 z2 的和等于复数 (a1 +a2) + i (b1 + b2)。

第一个复数的实部与第二个复数的实部相加。这意味着实部可以与另一个复数的实部相加。

同样，第一个复数的虚部与第二个复数的虚部相加。

Re (z1 + z2) = Re (z1) + Re (z2)

Im (z1 + z2) = Im (z1) + Im (z2)

让我们看几个例子。

示例 1：如果 z1 = (3x - 7) + 2iy 且 z2 = -5y + (5 + x) i。求 z1 + z2。

z1 + z2 = (3x - 7) + 2iy + (-5y + (5 + x) i)

z1 + z2 = 3x - 7 + 2iy - 5y + 5i + xi

z1 + z2 = 3x - 5y -7 + i(x + 2y + 5)

示例 2：如果 z1 = 5 + 4i 且 z2 =6 - 2i。求 z1 + z2。

z1 + z2 = 5 + 4i + 6 -2i

z1 + z2 = 11 + 2i

复数减法

设两个复数为 z1 和 z2，其中

z1 = a1 + ib1

z2 = a2 +ib2

复数 z2 从 z1 中减去表示为 z1 - z2。我们也可以将其定义为两个复数 z1 和 -z2 的加法。

同样，复数 z1 从 z2 中减去表示为 z2 - z1。它也等于 z2 + (-z1)。

让我们来看一些例子。

示例 1：求 z1 - z2，如果 z1 = 5 + 3i 且 z2 = 2 - 7i。

z1 - z2 = 5 + 3i - (2 - 7i)

= 5 + 3i - 2 + 7i

= 3 + 10i

z1 - z2 = 3 + 10i

示例 2：求 z1 - z2，如果 z1 = 4 + 3i (2i + 7) 且 z2 = 2 - 7i (2i + 6)。

z1 - z2 = 4 + 3i (2i - 7) - [2 - 7i (2i + 6)]

z1 - z2 = 4 + 6i^2 - 21i - [2 - 14i^2 - 42i]

z1 - z2 = 4 + 6i^2 - 21i - 2 + 14i^2 + 42i

z1 - z2 = 4 - 6 - 21i - 2 - 14 + 42i

z1 - z2 = -18 + 21i

复数乘法

首先，让我们理解两个复数 (a +bi) 和 (c+ di) 的乘法。

(a+bi)(c+di)=ac+adi+cbi+bdi²

(a+bi)(c+di)=ac+adi+cbi-bd

下面展示了两个复数的乘法过程

设两个复数为 z1 和 z2，其中

z1 = a1 + ib1

z2 = a2 +ib2

两个复数 z1 和 z2 的乘法表示为 z1z2。

z1z2 = (a1 + ib1)(a2 + ib2)

z1z2=a1a2+a1b2i+a2b1i+b1b2i²

z1z2=a1a2+a1b2i+a2b1i-b1b2

分离实部和虚部，

z1z2=(a1a2-b1b2)+i(a1b2+a2b1)

我们可以将上述方程写成

z1z2 = [Re (z1) Re (z2) - Im (z1) Im (z2)] + i[Re (z1) Im (z2) + Re (z2) Im (z1)]

让我们通过几个例子来理解。

示例 1：如果 z1 = 3 + 4i 且 z2 =6 + 7i。求 z1z2。

z1z2 = (3 + 4i) (6 + 7i)

z1z2 = 18 + 21i + 24i + 28i^2

z1z2 = 18 + 21i + 24i - 28

z1z2 = -10 + 45i

示例 2：如果 z1 = 3 - 4 (i + 4) 且 z2 =6 - 2i。求 z1z2。

z1z2 = (3 - 4 (i + 4)) (6 - 2i)

z1z2 = (3 - 4i -16) (6 - 2i)

z1z2 = (-13 - 4i) (6 - 2i)

z1z2 = -78 + 26i -24i + 8i^2

z1z2 = -78 + 26i -24i - 8

z1z2 = - -86 + 2i

复数除法

设复数为 z = a + ib。复数 z 除以一个非零复数 z1 可以表示为 z/z1。

我们也可以将 z 与 z1 的乘法逆元相乘。它也可以表示为 z/z1。

设 z = a + ib 且 z1 = a1 + ib1。

我们可以写成

让我们考虑一个例子。

示例 1：如果 z1 = 2 + 4i 且 z2 = 1 + 2i，求 z1/z2。

复数共轭

设复数为 z = a + bi。

复数 z 的共轭为 a - bi。

类似地，复数 2 + 4i 的共轭是 2 - 4i。

因此，共轭被定义为通过将 i 替换为 -i 而得到的数。

复数的模

复数 z 的模表示为 |z|。

其定义为

让我们来看一些例子。

示例 1：求 z = 3 - 4i 的模。

示例 2：求 z = 5 + i (6 -3i) 的模。

我们可以将上述复数写成

z = 5 + 6i + 3

i²=-1

z = 8 + 6i

复数的倒数

设 z = a + ib

我们将给定复数的分子和分母与其共轭相乘，如下所示

因此，复数 z 的乘法逆是 1/z。

我们可以说，一个非零复数 z 的乘法逆与其倒数相同。它由以下给出

这意味着复数的共轭除以其模的平方。

让我们来看一些例子。

示例 1：求复数 2 + 3i 的倒数。

因此，给定复数的倒数是

我们也可以使用公式直接计算值

其中，

|z| = 13

示例 2：求 5 - 2i 的倒数。

因此，给定复数的倒数是

复数的极坐标形式

设 z 为复数，其中 z = x +iy。它在平面上由点 P (x, y) 表示，如图所示

我们知道 z = x + iy。

将 x 和 y 的值代入上述方程，我们得到

z=|z|cosθ+|z|isinθ

z=|z|(cosθ+isinθ)

我们可以写成

z=r(cosθ+isinθ)

其中，

r=|z|

z 的这种形式称为极坐标形式。因此，z 的极坐标形式为

z=r[cos(2πn+θ)+isin(2πn+θ)]

其中，

r=|z|

n = 整数

θ=arg(z)

arg (z) 表示以逆时针方向测量的角度。它取决于点所在的四个象限之一。

下面展示了四个象限

设，

anglefordifferentqudrants=α

对于位于第一象限的点，

θ=α

对于位于第二象限的点，

θ=π-α

对于位于第三象限的点，

θ=-(π-α)

对于位于第四象限的点，

θ=-α

让我们来看一些例子。

示例 1：将复数 1 + i 写成极坐标形式。

复数的极坐标形式为

给定复数 (1 + i) 的 x 和 y 是 (1, 1)。

这意味着点 (1, 1) 位于第一象限。

第一象限的 arg (z) 为

θ=α

给定复数的极坐标形式为

示例 2：将复数 -1 - i 写成复数形式。

复数的极坐标形式为

z=r(cosθ+isinθ)

其中，

给定复数 (1 + i) 的 x 和 y 是 (-1, -1)。

这意味着点 (1, 1) 位于第三象限。

第三象限的 arg (z) 为

给定复数的极坐标形式为

z=√2

cos(-θ)=cos(θ)∧sin(-θ)=-sin(θ)

因此，上述极坐标形式可写为

z=√2

示例 3：将复数 1 - i 写成复数形式。

复数的极坐标形式为

给定复数 (1 + i) 的 x 和 y 是 (1, -1)。

这意味着点 (1, 1) 位于第四象限。

第四象限的 arg (z) 为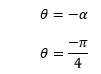

给定复数的极坐标形式为

z=√2

cos(-θ)=cos(θ)∧sin(-θ)=-sin(θ)

因此，上述极坐标形式可写为

z=√2

复数平方根

设 a + ib 为复数。

√a+ib=x+iy

其中 x 和 y 是实数。

上述方程可以计算为

√a+ib=x+iy

两边平方，我们得到

令虚部和实部相等，我们得到

a=x²-y²

b=2xy

我们可以将上述方程写成

让我们看几个例子。

示例 1：求复数 7 - 24i 的平方根。

我们假设，

现在，比较实部和虚部的值，我们得到

示例 2：求复数 -15 - 8i 的平方根。

我们假设，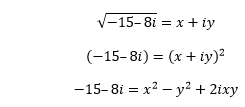

现在，比较实部和虚部的值，我们得到