圆锥体体积

在本节中，我们将学习什么是圆锥、圆锥的类型、圆锥体积的公式及其推导。此外，我们还将学习如何计算圆锥的体积。

圆锥

圆锥是一个三维几何形状，它有一个圆形底面（表面）和一个顶点。顶点通过两条倾斜的线段与底面连接。这两条线段连接在一个称为顶点的共同点上。冰淇淋蛋筒和生日帽是圆锥的最佳示例。下图显示了圆锥的形状。

• 顶点：圆锥顶点位于底面上方。
• 斜高：连接到顶点的倾斜线段的高度。用 l 表示。
• 高：从底面到顶点的垂直距离称为圆锥的高。也称为垂直高。用 h 表示。
• 底面：圆锥的圆形表面。
• 半径：圆心与圆周之间的距离称为半径。用 r 表示。

圆锥的类型

圆锥有两种类型

• 直圆锥或圆锥
• 斜圆锥

直圆锥或圆锥：顶点垂直于底面中心的圆锥。下图显示了直圆锥的形状。

斜圆锥：顶点不在底面中心正上方的圆锥称为斜圆锥。下图显示了斜圆锥的形状。

圆锥的体积

在数学中，物体所包围的面积称为该物体的体积。圆锥也是一个三维几何形状，因此圆锥所覆盖的面积称为圆锥的体积。用字母V表示。

注意：半径和高度必须使用相同的单位。如果单位不同，请在计算前进行转换。

体积单位

体积的单位是立方单位或单位³。

圆锥体积公式

半径为 (r) 的圆锥的体积 (V) 是底面积乘以高。换句话说，圆锥的体积是圆柱体积的三分之一。如果我们知道半径和高度，可以使用以下公式轻松计算圆锥的体积。

注意：上述公式也用于计算斜圆锥的体积。

如果圆柱和圆锥的高度相同，则圆柱的体积将是圆锥体积的三倍。

已知斜高 (l) 时圆锥的体积

公式推导

在上图中，我们有一个相同高度和半径的圆柱形和圆锥形。将圆锥形放入圆柱形内。现在向圆柱形中倒水。我们发现它并没有完全填满圆柱体。重复此过程两到三次后，我们发现同样的实验可以完全填满圆柱体。

因此，圆锥的体积等于圆柱体积的三分之一。

考虑上图，圆形底面的半径为 r，高度为 h。

我们知道圆柱的体积是底面积乘以其高度。

圆柱体积 (V) = 底面积 × 圆柱高度

V=πr² h

我们知道圆锥的体积等于圆柱体积的三分之一。因此，

圆锥体积 (V) = × 圆柱体积

其中

V：是圆锥的体积。

π：是一个常数，其值为 22/7 或 3.14。

r：是底面的半径。

h：是圆锥的垂直高度。

让我们看看如何计算圆锥的体积。

示例 1：圆锥的垂直高度为 15 厘米，半径为 4 厘米。计算圆锥的体积。（Pi = 3.14）

解决方案

已知，高度 (h) = 15 厘米

半径 (r) = 4 厘米

我们知道圆锥体积的公式

将值代入上述公式，我们得到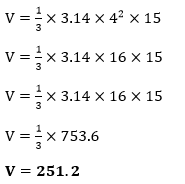

因此，圆锥的体积为 251.2 cm³。

示例 2：圆锥的直径为 10 米，高度为 19 米。计算体积并以图形方式表示。

解决方案

已知，高度 (h) = 19 米

直径 = 10 米

我们知道半径是直径的一半。因此，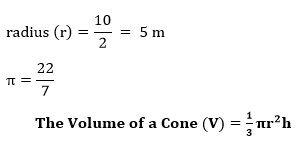

将值代入上述公式，我们得到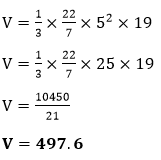

因此，圆锥的体积为 497.6 m³。

示例 3：生日帽的斜高为 30 厘米，底面半径为 12 厘米。计算体积。

解决方案

已知，斜高 (l) = 30 厘米

半径 (r) = 12 厘米

π = 3.14

我们知道已知斜高和半径时的体积公式。

将值代入上述公式，我们得到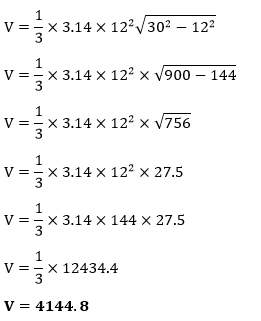

因此，圆锥的体积为 4144.8 cm³。

示例 4：管道体积为 223 m³。计算圆锥的体积。

解决方案

已知，圆柱体积 (V) = 223 m³

圆锥体积 (V) =？

我们知道圆锥的体积是圆柱体积的三分之一。因此，

V = × 223

V = 74.33

因此，圆锥的体积为 74.33 m³。

示例 5：如果圆锥和圆柱的高度均为 12 厘米，半径为 4 厘米，证明圆柱的体积是圆锥体积的三倍。

解决方案

已知，高度 (h) = 12 厘米

半径 (r) = 4 厘米

我们知道：

圆柱体积 (V) = πr² h

将值代入上述公式，我们得到

V = 3.14 × 4² × 12
V = 3.14 × 16 × 12
V = 602.88

我们也知道，

圆锥体积 (V) = × 圆柱体积

将值代入上述公式，我们得到

圆锥体积 (V) = × 602.88

圆锥体积 (V) = 200.96

为了验证答案，将圆锥的体积乘以 3，得到圆柱的体积。因此，

200.96 × 3 = 602.88

证明完毕。