梯形面积

梯形是一种凸四边形。它是一个有四条边且其中一对对边平行的封闭形状。

在本节中，我们将学习如何找到梯形的面积。

梯形 (Trapezoid)

四条边中有一对平行边的几何形状称为梯形。平行边称为底，非平行边称为腰。平行边可以是水平的、垂直的或倾斜的（对角的）。它也称为梯形。

在下图中，底₁和底₂垂直于虚线，虚线表示高。高是两底之间的距离。

梯形的性质

• 如果梯形的两对对边都平行，则它是一个平行四边形。
• 如果梯形的两对对边都平行；所有边都相等且相互垂直，则它是一个正方形。
• 如果梯形的两对对边都平行；对边相等且相互垂直，则它是一个矩形。
• 每个底边必须垂直于高。

梯形类型

梯形有三种类型

• 直角梯形：包含一对直角。
  
• 等腰梯形：非平行边长度相等的梯形。在下图中，边AD和BC长度相等。
  
• 不等边梯形：边长或角度都不相等的梯形。
  

梯形的不同形状是

要找到梯形的面积，请按照以下步骤操作

• 相加两条底边
• 将总和乘以高
• 将结果除以 2

梯形面积公式

梯形的面积是平均宽度乘以高。将其应用到公式中

或

或

其中b1和b2是每条底边的长度，h表示高。

梯形公式推导

让我们通过使用两个全等梯形组成的平行四边形来推导公式。

• 绘制一个底长为b1和b2、高为h的梯形。
• 创建它的一个副本。
• 将梯形副本旋转.
• 将梯形副本添加到原始梯形中。

当我们组合两个梯形（如上）时，它们会形成一个平行四边形。新形成的形状有两对全等的对边。

我们知道

平行四边形面积 (A) = b * h

这意味着平行四边形的面积是高乘以任意一条底边的长度。根据上图，两条底边的长度之和等于 b1 + b2。

根据平行四边形公式，我们得到

上面的面积是两个梯形的面积。因此，我们需要将其除以 2 才能得到一个梯形的面积。

梯形面积 (A) = (b1 + b2) * h / 2

重新排列上述公式，我们得到

计算梯形面积的另一种方法是将梯形分成两个三角形。

现在我们有两个三角形 ∆ABD 和 ∆BCD。我们将分别计算三角形的面积。两个三角形的总面积将是梯形的面积。

三角形面积

A = ½ b1 * h

三角形面积

A = ½ b2 * h

将面积相加，我们得到

A + A = ½ (b1 * h) + ½ (b2 * h)

2A = (b1 + b2) * h

A = 1/2 (b1 + b2) * h

示例

示例 1：如果一个梯形的底边分别为 30 英寸和 20 英寸。梯形的高为 4 英寸。求梯形的面积。

解决方案

已知 b1 = 30 英寸，b2 = 20 英寸，高 = 4 英寸

梯形面积 (A) = 1/2 (b1 + b2) * h

A = ½ (30 + 20) * 4

A = ½ (50) * 4

A = 200/2

A = 100 平方英寸

梯形的面积为 100 平方英寸。

示例 2：求给定梯形的面积。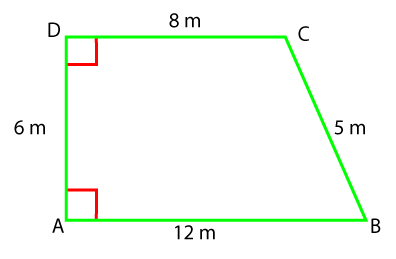

解决方案

从上图中，我们将只考虑平行边 AB 和 CD，因为它们与平行边成直角。

已知 b1=12 厘米，b2=8 厘米，h=6 厘米

我们知道：

A = h/2 (b1 + b2)

将值代入上述公式，我们得到

梯形的面积为 60 平方厘米。

示例 3：求一个梯形的面积，其底边分别为 10 米和 7 米。梯形的高为 5 米。求面积。

解决方案

首先，我们将梯形分成两个三角形，如上图所示。

现在分别求三角形的面积。我们知道

三角形面积 (A) = 1/2 b * h

∆ABC 的面积 = ½ (7 * 5)

A = 35/2

A = 17.5 平方米

类似地，∆CDA 的面积 = ½ (10 * 5)

A = 50/2

A = 25 平方米

将 ∆ABC 和 ∆CDA 的面积相加，即可得到梯形的总面积。

梯形面积 = ∆ABC 的面积 + ∆CDA 的面积

梯形面积 (A) = 17.5 + 25

A = 42.5 平方米

梯形的面积为 42.5 平方米。