数学中的积2025年3月17日 | 阅读 7 分钟 数学中的**积**是指乘法运算的结果。在本节中,我们将详细学习**积**这个术语及其**性质**和**示例**。 数学中的积是什么?**数学中的积**可以定义为**两个或多个数字相乘**。换句话说,是一个表示要相乘的因数的表达式。 积是我们将两个数**乘数**和**被乘数**相乘后得到的结果。 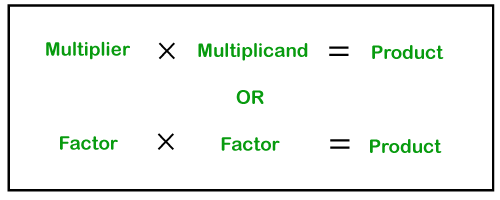 乘号**左边**的数字称为**乘数**,乘号**右边**的数字称为**被乘数**。乘数和被乘数都称为**因数**。 如何求积我们通过在两个或多个数字之间应用数学乘法运算**(× 或 * 或 .)**来得到两个数的积。例如 9×7=63 在这里,**63** 是 **9** 和 **7** 的**积**。 类似地, 4×5×8=160 在这里,**160** 是 **4、5** 和 **8** 的**积**。 我们还可以通过**重复加法**方法找到两个数的积。这意味着将数字本身加到乘数次。这种方法只适用于我们要找两个小数的积时。 a×b=b+b+b…+b 这意味着,将 **b** 加 **a** 次,反之亦然。 但这并非传统的乘法方法。例如,如果我们要找 **6** 和 **7** 的积,我们可以将数字 **6** 加**七**次。 6+6+6+6+6+6+6=42 或 7+7+7+7+7=42 将数字 6 和 7 相乘,我们得到相同的结果。 6×7=42 注意:在本节的最后,我们写了如何求两个两位数和两个三位数的积的步骤。两个整数的积整数包括正数和负数。乘数或被乘数在数字前可能带有**正**号或**负**号。数字前**没有符号**表示正数。如果数字带有正号或负号,它们遵循下表中的规则。 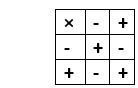 上表表示
让我们看一些基于上述规则的例子。 示例 15×5=75 -3×-9=27 -14×5=-70 6×-12=-72 两个小数的积小数是包含**小数点 (.)** 的数字。例如,**23.56** 是一个小数。 我们还可以使用以下步骤找到两个小数的积
示例:求 23.3 和 12.21 的积。 解决方案 问题中有两个小数 **23.3** 和 **12.21**。
两个分数的积分数是以**分子**和**分母**形式表示的数字。 为了求两个分数的积,将**乘数的分子**乘以**被乘数的分子**,并将**乘数的分母**乘以**被乘数的分母**。用公式表示,我们可以将上述陈述写为   **分数**与其**乘法逆元**的积始终为 1。假设,一个分数是  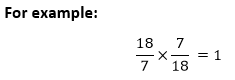 如果分数中没有分母,请始终视为**1**。数字 **3** 在分数形式中与 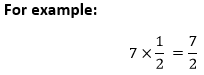 有时,如果分数可被分母整除,或者乘数的分子可被被乘数的分母整除,反之亦然,我们需要简化分数。 注意:分子和分母必须能被相同的数字整除。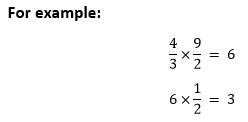 两个复数的积复数是可以表示为 **(a+bi) 或 (a-bi)** 形式的数字,其中 **a** 和 **b** 是**实数**,**i** 是**虚数**。 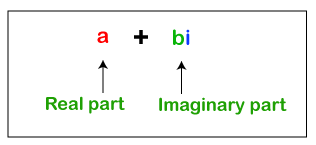 我们可以使用**分配律**找到两个复数的积。请记住以下关于 i 的要点。
一般来说,两个复数 **(a+bi)** 和 **(c+di)** 的积是  让我们看一个示例。 示例:求两个复数 (3-2i) 和 (-1+4i) 的积。 解决方案 (3-2i)×(-1+4i)=3×(-1)+3×(4i)-(2i)×(-1)-(2i)×(4i) 将 **i2=-1** 的值代入,我们得到 -3+14i-8×(-1) 两个复数 (3-2i) 和 (-1+4i) 的积是 (5+14i)。 平方根的积性质
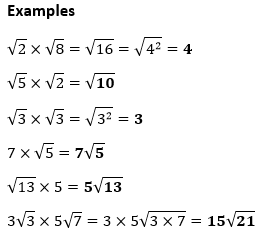 积的性质积有**四个**基本性质
结合律 当我们把三个或更多的数字乘在一起时,无论首先乘哪两个,乘积都相同。  交换律 乘法的顺序不影响乘积。  恒等性质 如果一个数字乘以 1,我们会得到相同的数字。因此,**1** 被称为**乘法单位元**。  分配律 这个性质被称为乘法对加法的分配律。它指出,如果一个和乘以一个数字,我们可以先将和的每一部分乘以这个数字,然后将结果相加。  积的一些其他性质是
两个大数的积一旦我们掌握了逻辑,就很容易记住。为了更好地理解,我们写出了两个大数相乘的步骤。 注意:以下方法适用于乘数和被乘数具有相同位数的情况。两个一位数的积为了找到两个一位数的积,我们必须记住**乘法口诀表**或**乘法表**到 10。这使得找到两个数的积变得容易。即使我们不使用笔和纸也能找到积。下表显示了 1 到 10 的乘法表。 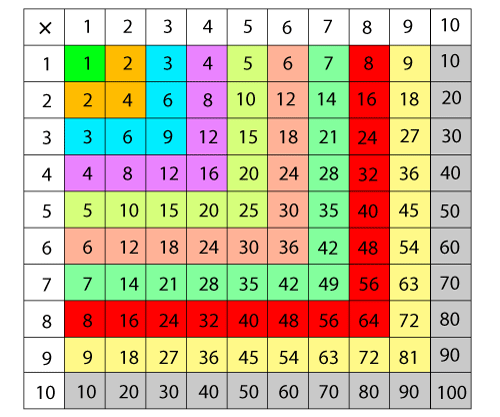 两个两位数的积这包括**三个**步骤。为了便于理解,我们在这里使用了**四个**字母 (a, b, c, d) 作为数字。 假设我们要计算 **ab×cd** 的积,那么我们必须遵循以下步骤 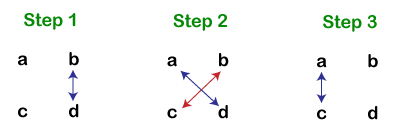 让我们在一个例子中实现上述步骤。 **示例:47×56 的积是多少?** 步骤 1: (b×d) 7×6=42 在答案中写 **2**,并将 **4** 作为进位到下一步。 (更新答案:2) **步骤 2:** [(a×d)+(b×c)]+上一步的进位(如果有) [(4×6)+(5×7)]+4=63 在答案中写 **3**,并将 **6** 作为进位到下一步。 (更新答案:32) **步骤 3:** (a×c)+上一步的进位(如果有) (4×5)+6=26 在答案中写 **26**。 (更新答案:2632) (47×56) 的积是 2632。 注意:始终从右到左写答案。两个三位数的积这包括**五个**步骤。为了便于理解,我们在这里使用了**六个**字母 (a, b, c, d, e, f) 作为数字。 假设我们要计算 abc×def 的积,那么我们必须遵循以下步骤 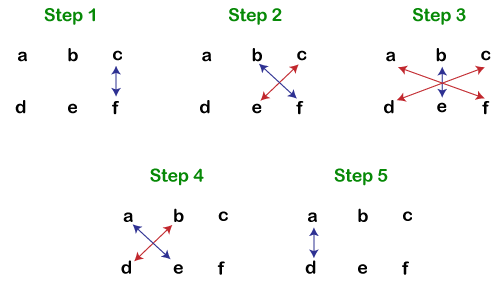 让我们在一个例子中实现上述步骤。 示例:624×315 的积是多少? **步骤 1:** (c×f) 4×5=20 在答案中写 **0**,并将 **2** 作为进位到下一步。 (更新答案:0) **步骤 2:** [(b×f)+(c×e)]+上一步的进位(如果有) [(2×5)+(4×1)]+2=16 在答案中写 **6**,并将 **1** 作为进位到下一步。 (更新答案:60) **步骤 3:** [(a×f)+(b×e)+(c×d)]+上一步的进位(如果有) [(6×5)+(2×1)+(4×3)]+1=45 在答案中写 **5**,并将 **4** 作为进位到下一步。 (更新答案:560) **步骤 4:** [(a×e)+(b×d)]+上一步的进位(如果有) [(6×1)+(2×3)]+4=16 在答案中写 **6**,并将 **1** 作为进位到下一步。 (更新答案:6560) **步骤 5:** (a×d)+上一步的进位(如果有) (6×3)+1=19 在答案中写 **19**。 (更新答案:196560) (624×315) 的积是 196560。 同样,我们也可以使用以下步骤找到**两个四位数**的积。 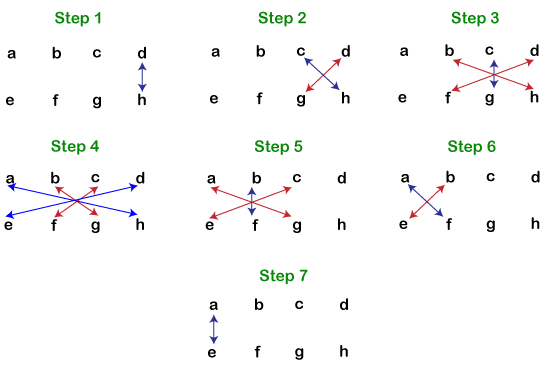 下一个主题数学中的函数 |
我们请求您订阅我们的新闻通讯以获取最新更新。