分数化简

化简或约分分数意味着将分数转换为最简形式。如果1是分数的分子和分母唯一的公因数，则称该分数是已化简的分数。要化简分数，请选择能完全除尽分子和分母的最大数。

如何化简分数

有三种方法可以化简分数

• 使用重复除法
• 使用最大公因数 (GCF)
• 使用质因数分解树

使用重复除法

在这种方法中，我们选择一个小数（例如2、3、4、5）来除一个分数。数字的选择由分数的特征来决定。

假设给出了分数 ，我们选择了数字5来除该分数。这将是一个错误的选择，因为它不能除尽任何一个数。如果选择3而不是5，那将是一个合适的数字。因此，数字的选择必须是适当的。

要化简分数，请遵循以下步骤：

• 选择一个小数。
• 用这个小数除分子和分母。它会生成一个新的分数，带有新的分子和分母。
• 如果新生成的分数仍然可以被那个小数除尽，则继续执行上一步。否则，选择一个不同的数字来除分数并转到上一步。
• 确保分数没有公因数。

例1：化简分数 。

解决方案

在分数 中，分子和分母都是偶数，所以我们选择2来除分数。

我们得到分数 ，它仍然可以被2除尽。所以，我们将再次用2除。

我们得到分数 ，它仍然可以被2除尽。所以，我们将再次用2除。

分数不能再进一步化简，因为3是质数，只能被1和它本身除尽。分母不能被3除尽。

因此，化简后的分数是。

例2：化简分数。

解决方案

在分数中，分子和分母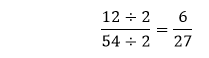都是偶数，所以我们选择2来除分数。

我们得到分数 ，它仍然可以被2除尽。所以，我们将再次用2除。

我们得到分数 ，其中分子可以被2除尽，但分母不能。所以，我们将选择一个不同的数字，它可以同时除尽分子和分母。因此，我们将用3除分数 。

分数 不能再进一步化简，因为2是质数，只能被1和它本身除尽。分母不能被2除尽。

因此，化简后的分数是 。

例3：化简分数 。

解决方案

在分数 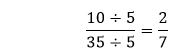中，分子和分母都可以被5除尽。所以，我们选择数字5来除分数。

分数不能再进一步化简，因为2是质数，只能被1和它本身除尽。分母不能被2除尽。

因此，化简后的分数是。

使用最大公因数 (GCF)

最大公因数是能完全除尽该数的数字。在约分分数时，重复用最大公因数除分子和分母很简单。如果分子和分母的最大公因数是1，则分数不能再进一步约分。这意味着分数处于最简形式。

要化简分数，请遵循以下步骤。

• 列出分子和分母的所有因数。
• 写出所有公因数。
• 找出最大公因数。
• 用最大公因数除分子和分母。
• 写出约分后的分数。

注意：每个数字都可以被1和它本身除尽。所以，1和数字本身是每个数字的两个因数。

让我们看一些例子。

例4：化简分数 。

解决方案

步骤1：分子(12)的因数：1, 2, 3, 4, 6, 12

           分母(18)的因数：1, 2, 3, 6, 9, 18

步骤2：公因数：1, 2, 3, 6

步骤3：最大公因数：6

步骤4：我们将用最大公因数，即6，除分子和分母。

我们不能再进一步化简分数，因为分子和分母都可以被自身除尽，并且最大公因数是1。

步骤5：因此，化简后的分数是 。

例5：化简分数 。

解决方案

步骤1：分子(25)的因数：1, 5, 25

           分母(75)的因数：1, 3, 5, 15, 25, 75

步骤2：公因数：1, 5, 25

步骤3：最大公因数：25

步骤4：我们将用最大公因数，即25，除分子和分母。

我们不能再进一步化简分数，因为分子和分母都可以被自身除尽，并且最大公因数是1。

步骤5：因此，化简后的分数是 。

例6：化简分数 。

解决方案

步骤1：分子(8)的因数：1, 2, 4, 8

分母(10)的因数：1, 2, 5, 10

步骤2：公因数：1, 2

步骤3：最大公因数：2

步骤4：我们将用最大公因数，即2，除分子和分母。

我们不能再进一步化简分数，因为分子和分母都可以被自身除尽，并且最大公因数是1。

步骤5：因此，化简后的分数是 。

例7：化简分数 。

解决方案

步骤1：分子(30)的因数：1, 2, 3, 5, 6, 10, 15, 30

分母(36)的因数：1, 2, 3, 4, 6, 9, 12, 18, 36

步骤2：公因数：1, 2, 3, 6

步骤3：最大公因数：6

步骤4：我们将用最大公因数，即6，除分子和分母。

我们不能再进一步化简分数，因为分子和分母都可以被自身除尽，并且最大公因数是1。

步骤5：因此，化简后的分数是 。

使用质因数分解树

在这种方法中，我们找出分子和分母的质因数并消去公因数。

质因数：质因数是只能被自身除尽的质数。例如，2、3、5、7、11等。要找出质因数，将给定的数字分解成两个数字，其中一个必须是质数。重复此过程，直到两个数字都是质数。

要使用质因数分解树化简分数，请遵循以下步骤。

• 确定分子和分母的质因数。
• 用乘法符号写出每个数字的质因数，例如 (2×2×3)。
• 消去分子和分母中共同的公因数。

让我们通过示例来理解。

例8：化简分数

解决方案

让我们找出24和60的质因数。

用乘法符号写出质因数。

消去公因数，我们得到

因此，化简后的分数是。

例9：化简分数。

解决方案

让我们找出820和240的质因数。

用乘法符号写出质因数。

消去公因数，我们得到

因此，化简后的分数是 。