1 到 99 的所有数字之和是多少？

等差数列是数字序列，其中任意两个连续数字之间的差是常数值。例如，自然数序列 1,2,3,4,5,6,8,...。该序列有一个公差。等差数列用符号表示。

数列的类型

在数学中，存在三种类型的数列，它们是

• 调和数列
• 等比数列
• 等差数列

等差数列用符号 AP 表示。

符号

在等差问题中使用了几个符号，它们是

前 n 项之和，S_n

首项 = a

公差 = d

首项 = (a)

第 n 项 = a_n

这些项显示了等差数列的属性。

等差数列的首项

等差数列也可以用公差的形式表示，如下所示。

a, a+d, a+2d, a+3d, a+4d ,....a+(n-1)d

这里的“a”代表首项。

a₁= a

a₂= a + d

a₃= a + 2d

等差数列中的公差

在一个数列中，给定的是公差：第 n 项和首项。假设数列开始为 a₁, a₂, ....a_n。

a₂-a₁= d

公差可以是负数、零或正数。

等差数列的通项公式

项位置 = 1

项的表示：a₁

项的值 = a = a + (1 - 1) d

项位置：2

n 项的表示 = a₂

项的值 = a +d = a + (2-1) d

= a + d

项位置 = 3

n 项的表示 = a₃

项的值 = a + (3 - 1) d

= a +2d

项位置 = 4

项的表示 = a₄

项的值 = a + 3d = a + (4 - 1) d

等差数列的公式

等差数列中使用了两个主要公式，它们与以下内容相关

• 前 n 项之和
• 等差数列的第 n 项

第 n 项的公式

a_n = a+(n-1)d

此处，

a_n= 第 n 项

首项 = a

公差 = d

项数 = n

不同类型的等差数列

• 有限等差数列： 包含有限项的数列称为有限等差数列。有限等差数列将包含最后一项。
  有限等差数列的例子包括 3, 5, 7, 9, 11, 13, 15, 17, 19, 21
• 无限等差数列： 不包含有限项的等差数列称为无限等差数列。它不包含最后一项。
  例如，2, 4, 6, 8, 10, 12, 14, 16, ....

n 项之和

假设一个等差数列包含“n”项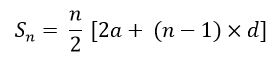

证明方法

假设一个等差数列包含“n”项，它们按顺序排列为 a, a + d, a + 2d, ....., a + (n -1) x d。

前 n 项之和 = a, a + d, a + 2d, ..., a + (n - 1) d ----------- (1)

逆序

S_n=[a+(n-1)×d] + [a+(n-2)×d] + [a+(n-3)×d] +...(a)- - - (ii)

上述方程的相加

2S_n = [ 2a + (n -1) × d] + [2a + (n -1) x d] + [2a + (n -1) x d] ...... + [ 2a + (n -1) x d ] ( n 项)

2S_n = n x [ 2a + (n - 1) x d]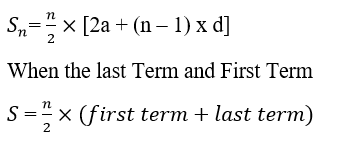

问题：1 到 99 的所有数字之和是多少？

答1, 2, 3, 4, 5, 6, 7, 9.... , 99

1 = a = 数列的首项

1 = d = 公差

99 = n = 项的总数

为了求和，我们将使用公式