1到50的平方数

平方，这个基本的数学概念，在数字领域占有重要地位。从数学的早期时代起，人类就被数字平方所展现的模式和性质所吸引。在本文中，我们将踏上一段探索平方世界的旅程，特别关注1到50之间数字的平方。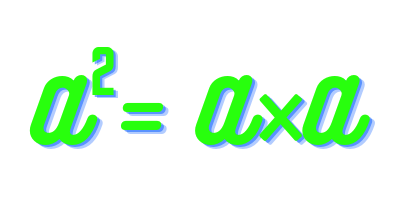

对一个数进行平方意味着将它乘以自身，结果就是它的平方。例如，3的平方是9（3² = 9），7的平方是49（7² = 49）。通过考察这个范围内的数字平方，我们旨在不仅展示数值结果，还阐明其潜在的关系和原理。

1到50的数字平方

模式与性质

• 平方数个位数的模式： 平方数在个位数上呈现出有趣的模式，揭示了它们的性质。通过识别这些模式，我们可以快速确定平方数的个位数，而无需计算整个平方。

示例

1. 个位数为1的平方数的个位数总是1。例如，1² = 1，11² = 121，21² = 441。
2. 个位数为4的平方数的个位数总是6。例如，4² = 16，14² = 196，24² = 576。
3. 个位数为5的平方数的个位数总是5。例如，5² = 25，15² = 225，25² = 625。
4. 个位数为6的平方数的个位数总是6。例如，6² = 36，16² = 256，26² = 676。
5. 个位数为9的平方数的个位数总是1。例如，9² = 81，19² = 361，29² = 841。

• 偶数平方与其一半平方的关系： 偶数的平方总是其一半平方的四倍。例如，(2 * n)² = 4 * (n²)，其中n代表任何正整数。

示例

例如，8的平方（2 * 8 = 16）是64，8的一半是4，4的平方是16。16的四倍等于64。

• 连续平方数之间的关系： 两个连续平方数之间的差总是等于这两个数的和。

示例

9和16之间的差是7，等于9 + 7。同样，16和25之间的差是9，等于16 + 9。

平方数的应用

平方数在各个领域都有实际应用，为测量、计算和问题解决提供了基础。

• 面积测量： 平方数在测量正方形和矩形的面积方面起着关键作用。正方形的面积通过其边长的平方计算。类似地，矩形的面积可以通过将其长和宽相乘来确定，长和宽通常用平方单位表示。
• 坐标系中的距离计算： 涉及到平方数的勾股定理，在坐标系中计算距离至关重要。当我们有两个点，由其坐标 (x₁, y₁) 和 (x₂, y₂) 表示时，它们之间的距离可以使用公式 √((x₂ - x₁)² + (y₂ - y₁)² ) 来计算。
• 理解二次方程： 二次方程在数学、物理和工程领域有广泛应用。二次方程包含平方项，如 ax² + bx + c = 0。求解这些方程通常需要操作和分析平方数。
• 数学模式和序列： 平方数是数学模式和序列中的基本元素，例如斐波那契数列和帕斯卡三角形。

结论

平方数在数学及其他领域提供了丰富的探索和理解空间。从其个位数中引人入胜的模式到它们与偶数和连续平方数的关系，平方数提供了对数学结构的迷人洞察。此外，它们在测量、坐标系和二次方程等领域的实际应用突出了它们在现实世界中的相关性。拥抱平方数的世界将为问题解决、测量和智力成长开启无限可能。