基本比例定理与相似三角形

几何学是数学的一个分支，研究形状和图形的性质与关系；这是一个几个世纪以来一直吸引着思想家和学习者的概念。“比例”是几何学中最基本的原理之一，在理解三角形和其他几何形状的性质方面非常重要。“基本比例定理”（BPT）是该概念的核心；它是一个基本结果，显示了三角形中线段的关系。该定理也称为“泰勒斯定理”，以著名的希腊数学家泰勒斯的名字命名。因此，在本文中，我们将了解基本比例定理的概念，探讨其重要性、证明和应用，并在文章结尾进行总结。

相似三角形

在学习基本比例定理或泰勒斯定理之前，我们需要对相似三角形有一个基本了解，因为该定理是基于相似三角形的概念；因此，我们可以说，如果两个三角形遵循以下两个性质，则它们是相似的，如下所述：

1. 如果三角形的所有边都成比例。
2. 如果所有对应于另一个三角形的角都相等。

因此，我们可以说，当两个三角形 XYZ 和 EFG 相似时，

XY / EF = YZ / FG = XZ / EG

角 X = 角 E，角 Y = 角 F，角 Z = 角 G

理解几何学中的比例

在我们理解基本比例定理之前，了解几何学中的比例概念很重要。在几何学中，比例是指比率的相等；比例通常表示为两个相等的比率。当我们说 a, b, c, d 成比例时，我们可以写成

a / b = c / d

这里，'a 和 b' 是一对量，'c 和 d' 是另一对量；在几何学语境中，这些量通常是形状或图形内的长度或线段。比例用于显示这些长度之间的关系，并且对于解决各种几何问题很重要。

几何学中的比例源于相似图形的概念；当两个图形具有相同的形状但大小可能不同时，它们就被认为是相似的。当两个图形相似时，它们的对应边成比例；换句话说，对应边长度的比率相等。现在我们已经理解了几何学中的比例，让我们来探讨基本比例定理。

基本比例定理

基本比例定理，通常称为泰勒斯定理，是几何学中的一个基本结果，它处理三角形内线段的比例；它指出“如果一条线平行于三角形的一条边，并与另外两条边相交，那么这条线将成比例地分割这两条边。”

该定理为分析和解决涉及三角形和平行线的问题提供了有力的工具；为了说明该定理，我们可以考虑一个三角形 ABC，其中一条线 DE 平行于边 BC，分别在 D 和 E 两点与边 AB 和 AC 相交。

在这个概念中，基本比例定理断言

AD / DB = AE / EC

换句话说，线段 AD 到线段 DB 的比率等于线段 AE 到线段 EC 的比率；只要线 DE 平行于边 BC，这种比例就会保持一致。

基本比例定理的证明

在本段中，我们将尝试证明基本比例定理；为此，我们首先要考虑图中所示的三角形 ABC。在该三角形中，**LM 线平行于 BC 线**，并与三角形 ABC 的边相交，L 在边 AB 上，M 在边 AC 上。

证明：根据基本比例定理，我们必须证明 AL / LB = AM / MC。

构造：在三角形 ABC 中，将顶点 B 连接到 M，同样，将顶点 C 连接到 L，形成直线 BM 和 CM，然后从点 L 向边 AM 作垂线 LY，从点 M 向边 AL 作垂线 MX，如下图所示。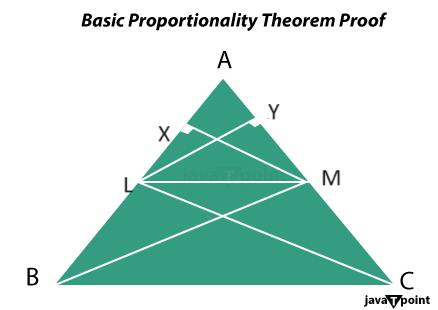

证明：三角形的面积等于该三角形底乘以高的一半，即 1 / 2 x 底 x 高。

所以，三角形 ALM 的面积 = 1 / 2 x AL x MX

三角形 LBM 的面积 = 1 / 2 x LB x MX

三角形 ALM 的面积 = 1 / 2 x AM x LY

三角形 LMC 的面积 = 1 / 2 x MC x LY

因此，三角形 ALM 和三角形 LMB 的面积比

三角形 ALM 的面积 / 三角形 LBM 的面积 = (1/2 x AL x MX) / (1/2 x LB x MX)

三角形 ALM 的面积 / 三角形 LBM 的面积 = AL / LB … (1)

因此，三角形 ALM 和三角形 LMC 的面积比

三角形 ALM 的面积 / 三角形 LBC 的面积 = (1/2 x AM x LY) / (1/2 x MC x LY)

三角形 ALM 的面积 / 三角形 LBC 的面积 = AM / MC … (2)

根据三角形的性质，在同一底边上且在两条平行线之间的三角形面积都相等。

因此，这意味着三角形 LBM 的面积等于三角形 LMC 的面积，即三角形 LBM 的面积 = 三角形 LMC 的面积 … (3)

因此，从方程 (1)、(2) 和 (3) 中，我们得出结论：

AL / LB = AM / MC

这就是我们要证明的。

基本比例定理的逆定理

在本段中，我们将证明泰勒斯定理或基本比例定理的逆定理，它指出如果我们画一条线分割三角形的边并使它们成比例，那么这条线将平行于三角形的第三条边。为了证明这一点，首先考虑一个三角形 ABC，其中 E 和 D 是三角形边上的两个点，E 位于 AC 边上，D 位于 AB 边上，直线 DE 将三角形的边分割成比例，使得

AD / BD = AE / CE … (1)

证明：我们必须证明直线 DE 平行于三角形的底边 BC，即 DE || BC。

构造：为了证明这一点，让我们画一条线 DE`，使得 DE` 平行于 BC，即 DE` || BC。如下图所示：

证明：正如我们所构造的，DE` 在三角形 ABC 中平行于 BC。

因此，根据基本比例定理，我们可以写出

AD / BD = AE` / CE` … (2)

从方程 (1) 和 (2) 中，我们可以说

AE / CE = AE` / CE`

将方程两边同时加一 (1)，我们得到

AE / CE + 1 = AE` / CE` + 1

(AE + CE) / CE = (AE` + CE`) / CE`

AC / CE = AC / CE`

CE = CE`

除非点 E 和 E` 是同一点，否则这是不可能的，因此我们可以得出结论，点 E 和 E` 是同一点。

这意味着 DE 平行于 BC，即 DE || BC，这就是我们要证明的。

基本比例定理的应用

基本比例定理在几何学中有广泛的应用，它为解决涉及三角形和平行线的各种问题提供了有价值的工具。下面讨论一些常见应用：

1. 平行线与截线：该定理通常用于通过显示它们成比例地分割三角形的边来证明某些线彼此平行；例如，如果你有一条截线与两条平行线相交，你可以使用该定理来证明在截线上形成的线段成比例。
2. 相似三角形：该定理与相似三角形的概念密切相关，因此它用于通过显示对应边和其他因素的比例来证明两个三角形相似。
3. 几何构造：该定理可用于几何构造中，将线段分成比例部分；这在创建具有特定比例的几何图形时特别有用（看起来也很不错）。
4. 计算未知长度：当你知道三角形中的某些比例并知道一条边的长度时，你可以使用基本比例定理来计算三角形内其他边或线段的长度。
5. 坐标几何：该定理可以应用于坐标几何，以确定笛卡尔平面中直线和点的坐标或方程。
6. 三角学：在三角学中，基本比例定理是处理三角形及其边长和角度时的基本概念。

一些常见问题

问：您对基本比例定理的理解是什么？

回答：基本比例定理，通常简称为BPT，是处理三角形内线段比例的基本几何原理；它指出，如果一条线平行于三角形的一条边，在另外两条边上相交于不同点，则该线将以相同的比例分割这两条边。换句话说，只要线平行于三角形的第三条边，这两条边上的对应线段长度的比率就保持不变；该定理在几何学中非常重要，尤其适用于证明平行性和相似性。

问：谁发现了基本比例定理？

回答：基本比例定理，也称为泰勒斯定理，由著名的希腊数学家“泰勒斯”提出；因此，为了纪念他，该定理通常被称为“泰勒斯定理”。泰勒斯，大约生活在公元前 624-548 年，他对几何学做出了七项重要贡献，他被认为是历史上最早的数学家之一。

问：BPT（基本比例）定理的推论是什么？

回答：基本比例定理 (BPT) 的推论指出，如果一条线以相同的比例分割三角形的两条边，那么这条线平行于三角形的第三条边；换句话说，当一条线与三角形的两条边相交，使得它在这些边上形成的线段的比率恒定时，这意味着这条线平行于三角形的剩余边。

问：基本比例定理还有其他名称吗？

回答：基本比例定理 (BPT) 的另一个名称是泰勒斯定理。为了纪念古希腊数学家泰勒斯，通常使用这个名字；它描述了当一条线平行于三角形的一条边并与另一条边相交于不同点时，三角形内线段的比例。泰勒斯对几何学的贡献产生了持久的影响，他的名字与几个（特别是七个）基本定理相关联。

问：两个三角形相似的条件是什么？

回答：要使两个三角形相似，必须满足两个条件：

1. 两个三角形的对应角相等：这意味着三角形顶点的角必须具有相同的度数；对应角在两个三角形中占据相同相对位置。
2. 两个三角形的对应边成比例：这个条件意味着两个三角形中对应边长度的比率相等。换句话说，如果你从两个三角形中选取任意一对边，它们的长度比率必须相同。

问：当两个三角形相似时，它们的大小是否必须相同？

回答：相似三角形不必具有相同的大小；虽然它们具有相同的形状，但它们的大小可以不同。相似三角形的关键特性是它们的对应边长度的比率相等。这意味着我们可以均匀地放大或缩小一个三角形来得到另一个三角形；换句话说，相似三角形在大小上是成比例的，但不一定是全等的，全等意味着同时具有相同的形状和相同的大小。相似三角形是几何学和三角学的基础，通常用于解决涉及间接测量和比例的问题。

结论

基本比例定理，也称为泰勒斯定理，是几何学中的基本且非常重要的定理；它的简洁性使其成为理解三角形和其他几何图形内线段比例的宝贵工具。通过为证明比率相等提供基础，该定理在解决广泛的几何问题中起着至关重要的作用，从证明线段平行到证明三角形相似；它的应用远远超出课堂，在建筑、工程和测量等各个领域都有用武之地。作为几何学中的基本原理，基本比例定理提醒我们数学概念在展示我们周围世界的奥秘方面的力量和美丽。