1 mod 4 等于多少

在模算术中，同余关系在理解数字之间的模式和关系方面起着至关重要的作用。其中一个同余关系是“1 mod 4”。本文将探讨 1 mod 4 的概念，并深入探讨其性质、应用以及在各种数学背景下的重要性。通过阅读本文，您将全面了解这种引人入胜的数学关系。

理解模算术

在我们深入了解 1 mod 4 的具体内容之前，让我们首先掌握模算术的基础知识。在这个数学分支中，数字根据它们除以给定模数后的余数被分成等价类。模数作为固定数字，决定每个等价类的大小。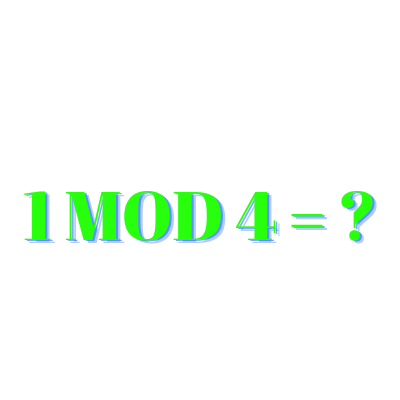

符号“a ≡ b (mod m)”表示 a 和 b 除以 m 时具有相同的余数。在“1 mod 4”的情况下，这意味着除以 4 余 1 的数字属于同一个等价类。

探索同余关系 1 mod 4

在 1 mod 4 的背景下，当我们检查这个等价类中的数字时，会遇到一个引人入胜的模式。考虑以下数字序列：

1, 5, 9, 13, 17, 21, 25, 29, 33, 37, ...

请注意，序列中的每个数字都比前一个数字大 4 个单位。这种模式无限期地持续下去。我们可以用代数形式表示这种模式，如下所示：

1 + 4k，其中 k 是一个整数。

1 mod 4 的性质

加法和减法：当我们执行涉及同余关系 1 mod 4 中数字的加法或减法运算时，结果保持在同一个等价类中。例如，(1 + 5) mod 4 = 2，(13 - 9) mod 4 = 4。

• 乘法：当我们用 1 mod 4 等价类中的一个数字乘以另一个数字时，结果仍然在该类中。例如，(1 * 5) mod 4 = 1，(9 * 13) mod 4 = 1。
• 除法：模算术中的除法可能有点复杂。然而，值得注意的是，并非同余关系 1 mod 4 中的所有数字都在同一个等价类中具有乘法逆元。换句话说，并非此类别中的所有数字都可以被同一类别中的另一个数字整除。

模算术的应用

• 密码学：模算术，包括同余关系 1 mod 4，在密码学算法中有着广泛的应用。密码系统利用模算术来确保安全的通信和数据加密。理解同余关系有助于这些密码系统的设计和分析。
• 数论：同余关系是数论的基础，数论研究整数的性质和关系。同余关系的研究使研究人员能够调查素数、模幂运算以及其他复杂的数论概念。
• 计算机科学：模算术，包括 1 mod 4，在计算机科学和编程中大量使用。它能够高效地计算大数、处理循环数据结构以及需要周期性或重复模式的各种算法。
• 序列和数列：同余关系经常出现在序列和数列的研究中。同余关系 1 mod 4 也不例外。分析这种关系使数学家能够识别模式、推导一般公式并预测序列和数列的行为。

重要性和进一步探索

同余关系在模算术和各种数学领域中占有重要地位。它的可预测模式和代数表示使其成为解决问题、建立联系和揭示隐藏关系的宝贵工具。

探索诸如 1 mod 4 之类的同余关系可以导致进一步的调查和发现。数学家经常将这些关系推广到更高的模数或探索不同的同余类，以揭示新的模式和见解。此类探索有助于数论、密码学和计算机科学的进步。

结论

同余关系 1 mod 4 为模算术的世界提供了引人入胜的见解。理解其性质、应用和重要性不仅增强了我们的数学知识，还使我们能够将其与其他领域（如密码学、数论和计算机科学）联系起来。通过深入研究此等价类中数字的模式和行为，我们揭示了模算术的复杂性，并开启了新的探索途径。因此，下次您遇到“1 mod 4”这个符号时，请记住它代表着一个等待被发现和理解的模式世界。