如何计算没有高的情况下三角形的面积

三角形的面积是其三条边所围成的空间。它可以根据三角形已知的尺寸和角度使用各种方法计算。一种简单的方法是当我们知道三角形的底和高时。但是，有时我们必须在不知道其高的情况下找到三角形的面积。在本文中，我们将学习如何做到这一点。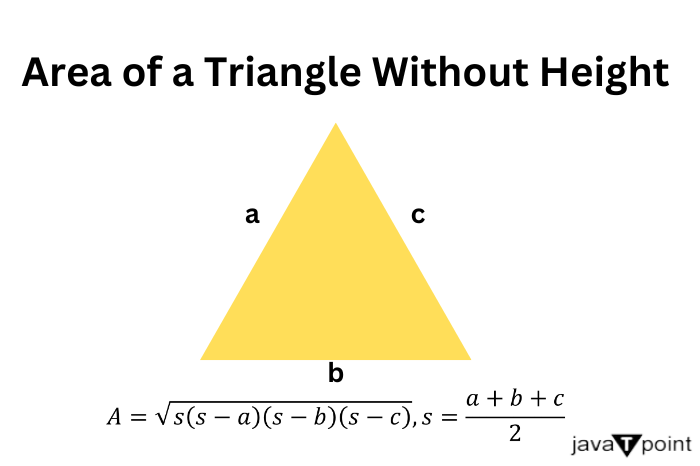

已知高的情况下三角形的面积

找到三角形面积最简单的方法是当已知其底和高时。使用底和高找到三角形面积的公式是

示例： 找到底为 6 厘米，高为 7 厘米的三角形的面积。

解决方案

三角形面积 = ½ * 底 * 高

= ½ * 6 厘米 * 7 厘米

= 3 厘米 * 7 厘米

= 21 平方厘米

没有高的等边三角形面积

我们可以在不知道等边三角形高的情况下，通过使用边长来找到其面积。边长为 a 的等边三角形的面积公式是

示例： 找到边长为 8 厘米的等边三角形的面积。

解决方案

等边三角形面积 = √3/4 * a^2

= √3/4 * 8^2

= √3/4 * 64

= 16√3 平方厘米

没有高的等腰三角形面积

我们可以在不知道等腰三角形高的情况下，通过使用边长来找到其面积。等腰三角形的面积公式，其中等边长度为 a，底边长度为 b，是

此公式是通过将等腰三角形分成两个直角三角形并使用勾股定理求其高来推导的。

示例： 找到等边为 8 厘米，底边为 10 厘米的等腰三角形的面积。

解决方案

面积 = ¼ * 10 * √(4a^2 - b^2)

= ¼ * 10 * √(4 * 8^2 - 10^2)

= ¼ * 10 * √(4 * 64 - 100)

= ¼ * 10 * √(256 - 100)

= ¼ * 10 * √156

= ¼ * 10 * 2√39

= 5 * √39

= 5√39 平方厘米

海伦公式计算没有高的三角形面积

海伦公式，以古希腊数学家亚历山大港的赫伦命名，用于在已知所有三条边长的情况下找到三角形的面积。它用于我们知道三角形边长但不知道其高的情况。用边长 a、b 和 c 计算三角形面积的海伦公式是

这里，s 是三角形的半周长，计算方法是：

示例： 找到边长为 7 厘米、24 厘米和 25 厘米的三角形的面积。

解决方案

半周长 (s) = (a + b + c)/2

= (7 厘米 + 24 厘米 + 25 厘米)/2

= 56/2

= 28 厘米

面积 = √(s * (s - a) * (s - b) * (s - c))

= √(28 * (28 - 7) * (28 - 24) * (28 - 25))

= √(28 * 21 * 4 * 3)

= √7056

= 84 平方厘米

已知两边和夹角计算三角形面积

要找到已知两边长度和它们之间夹角时三角形的面积，我们可以使用以下公式

其中

• a 和 b 是两边的长度
• C 是 a 和 b 之间夹角的度数

示例： 边长为 5 厘米和 7 厘米，夹角为 30 度的三角形的面积是多少？

解决方案

面积 = ½ * a * b * sin(C)

= ½ * 5 * 7 * sin(30)

= ½ * 35 * ½

= 35/4

= 8.75 平方厘米

结论

三角形的面积是其三条边所围成的空间。根据三角形已知的尺寸和角度，可以使用各种方法计算其面积。虽然最简单的方法是使用三角形的底和高，但当高未知时，可以应用其他方法。这些方法包括使用底和边长、海伦公式和三角函数。