三角形面积

在本节中，我们将详细学习三角形的定义、三角形的种类、三角形面积公式、推导以及如何求三角形的面积，并附带例子。

三角形

三角形是由三个顶点和三条边组成的。三个内角的和是180度。下图代表一个三角形。

三角形的种类

三角形有三种类型

• 等边三角形
• 等腰三角形
• 不等边三角形

等边三角形

等边三角形有三条等长的边和三个相等的角。每个角都是60度。它有三条对称轴。

等腰三角形

等腰三角形有两条等长的边和两个相等的角。它有一条对称轴。

不等边三角形

不等边三角形没有等长的边，也没有相等的角。它没有对称轴。

三角形面积

三角形的面积是三角形所覆盖的区域。三角形的面积等于底乘以高的一半。

如果给定的三角形是直角三角形，则将直角旁边的两条边相乘。

如果给定的三角形不是直角三角形，则首先通过从三角形最高点到底部画一条垂直线来找到三角形的垂高，如我们在下图所示。

三角形面积公式

两种公式用于计算三角形的面积。

它是底乘以高的一半。下面的公式适用于所有三角形。

三角形面积 (A) = 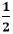bh

其中b表示底，h表示给定三角形的高。

注意：我们可以选择三角形的任何一边作为底，但要确保高是垂直于底测量的。

海伦公式

当已知三角形三条边的长度，或者三条边不相等时，就应用海伦公式。

它包含两个重要步骤

步骤 1：首先，将三角形三条边的长度相加，然后除以2，计算出半周长 (s)。

其中 a, b, c 是边的长度。

步骤 2：将半周长和三角形的三条边 a, b, c 代入公式，计算三角形的面积。

当已知两条边和一个角时，我们也可以求三角形的面积。但海伦公式不适用于这种情况。公式取决于已知哪些边和角。让我们看看不同边和角的情况下的公式。

• 当已知边 a, b 和角 C 时，三角形面积的公式是

三角形面积 (A) = ½ ab sin C

• 当已知边 b, c, 和角 A 时，三角形面积的公式是

三角形面积 (A) = ½ bc sin A

• 同理，当已知边 c, a, 和角 B 时，三角形面积的公式是

三角形面积 (A) = ½ ca sin B

等边三角形的面积

等边三角形有三条等长的边。

等边三角形面积 (A) = a²

其中 a 是三角形的边长。

等腰三角形的面积

推导

让我们看看为什么三角形的面积是 b*h 的一半。

• 画一个底为 b，高为 h 的三角形，如下图所示。

• 将三角形复制一份。

• 在新创建的三角形中，画一条垂线。

• 剪下三角形（黄色部分）并将其移到右侧，如下图所示。

我们看到三角形现在变成了一个矩形。我们知道矩形面积的公式

即 (b*h)。

底乘以高是三角形（蓝色部分）面积的两倍。但我们要计算的是三角形的面积，即

A = 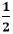bh

因此，三角形的面积是底乘以高的一半。

因此，三角形的面积是底乘以高的一半。

如何求三角形的面积

已知底和高

示例 1：求一个高为 20 厘米，底为 15 厘米的三角形的面积。

解决方案

Given, base (b) = 15 cm, height (h) = 20 cm

我们知道：

三角形面积 (A) = ½ bh

代入数值，我们得到

A = ½ 15 * 20
A = 150 平方厘米。

三角形的面积是 150 平方厘米。

示例 2：求下图所示三角形的面积。

解决方案

已知，底 (b) = 9 米，高 (h) = 13 米

我们知道：

三角形面积 (A) = ½ bh

代入数值，我们得到

A = ½ 9 * 13
A = 58.5 m²

三角形的面积是 58.5 m²。

示例 3：一个钝角三角形的底是 6.6 英寸，高是 14.7 英寸。求三角形的面积。

解决方案

已知，底 (b) = 6.6 英寸，高 (h) = 14.7 英寸

我们知道：

三角形面积 (A) = ½ bh

代入数值，我们得到

A = ½ 6.6 * 14.7
A = 48.51 英寸²

三角形的面积是 48.51 英寸²。

示例 4：求下图所示三角形的面积。

解决方案

从上图可知，底 (b) = 177 厘米。

注意：我们将考虑与底成直角的高，即 100 厘米。我们不会考虑 130 作为高，因为它与底不成直角。

我们知道：

三角形面积 (A) = ½ bh

代入数值，我们得到

A = ½ 177 * 100
A = 8850 平方厘米

三角形的面积是 8850 平方厘米。

已知三边长度

示例 5：求一个三边长都为 7 厘米的三角形的面积。

解决方案

已知，a = 7 厘米，b = 9 厘米，c = 11 厘米

这个问题已知三条边的长度。所以，我们将应用海伦公式。

三角形面积 (A) = √(s (s-a)(s-b)(s-c) )

首先，我们将计算半周长 (s)。

s = (7 + 9 + 11) / 2

s = 13.5 厘米

将值代入上述公式，我们得到

A = √(13.5 (13.5-7)(13.5-9)(13.5-11) )

A = √(13.5 (6.5)(4.5)(2.5) )

A = √987.1875

A = 31.41 平方厘米。

三角形的面积是 31.41 平方厘米。

已知 SAS（边-角-边）

示例 6：求一块三角形土地的面积，其中边 AB 为 125 米，边 BC 为 220 米。AB 和 BC 之间的夹角为 。

解决方案

首先，根据已知信息画一个三角形

已知，BC = a= 220 米，AB = c = 125 米，角 B = 123°

我们知道：

三角形面积 (A) = ½ ac sin B

A = ½ (220 * 125) * (sin )

A = ½ (27500) * (0.83867)

A = ½ (23063.4407)

A = 11,532 m²

三角形的面积是 11,532 m²。

示例 7：求下图所示三角形的面积。

解决方案

已知，CB = a = 9 厘米，AC = b = 14 厘米，角 C 是 25°

我们知道：

三角形面积 (A) = ½ ab sin C

A = ½ (9 * 14) * (sin 25°)

A = ½ (126) * (0.42261)

A = ½ (53.24886)

A = 27 厘米²

三角形的面积是 27 厘米²。

等边三角形的面积

示例 8：在一个等边三角形中，一条边长为十厘米，求该三角形的面积。

解决方案

已知，a = 10 厘米

我们知道等边三角形面积的公式

---

下一个话题摄氏度转华氏度

← 上一个 下一个 →