分数转小数

在本节中，我们将学习如何将分数转换为小数。在进行转换之前，让我们快速回顾一下分数和小数。

分数

分数以分子和分母的形式表示小数，即 。这是一种表达小数的方式。分数的另一个名称是有理数。分数有两种类型

• 假分数
• 带分数

假分数

分子大于分母的分数称为假分数。例如，。

带分数

带分数是一个数字，形式为 a，其中 a 是整数部分，是分数部分。在处理带分数时，首先将其转换为假分数。如果你想将带分数转换为假分数，请遵循以下步骤

• 将整数(a)乘以分母(c)。结果为 (a×c)。
• 在上面的结果 (a×c) 中，加上分子(b)。加上分子后，我们得到假分数的分子。
• 假分数的分母将是带分数的分母。

总的来说，我们可以说

十进制

小数是一个带有小数点(.)的数字。小数部分分隔整数部分和小数部分。这是表示分数的另一种方式。它不是一个整数。例如，22.96, 1.657, 987.09877 等。

如果小数的十进制小数点后有任何数量的零，则将其视为整数。因为小数点后的零不会影响值。例如，56.0000 与 56 相同。但是 56.00001 与 56 不相同。

让我们看一下下面的小数位值表。

在上面的表格中，我们观察到当向小数点左侧移动时，值会变大十倍，而当向小数点右侧移动时，值会变小十倍。

我们以一个小数为例，了解它的含义。

分数转小数

有三种方法可以将分数转换为小数。

• 使用计算器
• 展开分母法
• 长除法

使用计算器

这是将分数转换为小数的最简单方法。将分子除以分母，然后得到小数形式的答案。

示例 1：将分数 转换为小数。

解决方案

在计算器上，依次按下9、/、和7键。之后，按下等于键即可得到答案。

展开分母法

步骤 1：找到可以将分母转换为10 的幂的数字。这意味着一个数字可以将分母转换为10、100或1000。简而言之，即1 后面跟着 0。

步骤 2：将分子和分母乘以我们上面得到的相同数字。

步骤 3：计算分母中的0的数量，并在分子的右侧从右侧数相同的位数放置小数点。

让我们通过示例来理解。

示例 2： 的小数值是多少？

解决方案

在给定的分数中，9 是分子，5 是分母。

步骤 1：我们可以通过乘以2将分母转换为 10 的幂。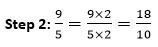

步骤 3：分母只有一个 0，所以我们从右侧数一位数字后，在分子中放置小数点。即 1.8。

因此，分数 的小数是 1.8。

示例 3：求 的小数值。

解决方案

在给定的分数中，35 是分子，4 是分母。

步骤 1：我们可以通过乘以25将分母转换为 10 的幂。

步骤 3：分母有两个 0，所以我们从右侧数两位数字后，在分子中放置小数点。即 8.75。

因此，分数 的小数是 8.75。

示例 4：求 的小数值。

解决方案

在给定的分数中，99 是分子，8 是分母。

步骤 1：我们可以通过乘以125将分母转换为 10 的幂。

步骤 3：分母有三个 0，所以我们从右侧数三位数字后，在分子中放置小数点。即 12.375。

因此，分数 的小数是 12.375。

示例 5：求 的小数值。

解决方案

在给定的分数中，225 是分子，16 是分母。

步骤 1：我们可以通过乘以625将分母转换为 10 的幂。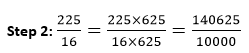

步骤 3：分母有四个 0，所以我们从右侧数四位数字后，在分子中放置小数点。即 14.0625。

因此，分数 的小数是 14.0625。

长除法

这是将分数转换为小数的另一种方法。它与我们除以两个数字相同，但由于增加了 0 而有点棘手。我们可以使用此方法来查找小数位数。

示例 6：求 的小数值。

解决方案

步骤 1：5 能整除 8，因为 1 乘以 5 等于 5。将 5 从 8 中减去，余数为 3。

步骤 2：5 太大了，无法整除 3，所以我们摆脱余数的唯一方法是在十分位上使用一个 0，这使得我们正在除的数字看起来像 80。现在我们可以将这个额外的 0 拉下来，使余数看起来像 30。

步骤 3：5 能整除 30，因为 5 乘以 6 等于 30，余数为 0。

因此，分数 的小数是 1.6。

示例 7： 的小数值是多少？

解决方案

4 太大了，无法整除 3。

步骤 1：让我们在 3 后面放一个小数点，在十分位上放一个零，使其变为 3.0。现在它类似于 30 除以 4。

步骤 2：4 能整除 30，因为 7 乘以 4 等于 28。将 28 从 30 中减去，余数为 2。

步骤 3：4 太大了，无法整除 2，所以我们摆脱余数的唯一方法是在百分位上使用另一个 0，这使得我们正在除的数字看起来像 300。现在我们可以将这个额外的 0 拉下来，使余数看起来像 20。

步骤 4：4 能整除 20，因为 5 乘以 4 等于 20，余数为 0。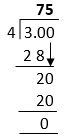

步骤 5：在答案中包含一个小数点。如果我们像这样保持列对齐，您会看到小数点就在这里。这使得我们的答案是0.75。

因此，分数 的小数是 0.75。

示例 8：将分数 转换为小数。

解决方案

因此，分数 的小数是 0.625。

示例 9：求 的小数值。

解决方案

在上面的例子中，我们看到它一次又一次地留下余数 1。看起来它可能会一直继续下去。所以，有些分数可能是这种类型。如果我们除它们，我们会看到数字不断重复的模式。

所以， 的小数值是0.3333……，3 会一直继续下去。但我们不能一直写 3。我们可以停止它们并四舍五入数字。这意味着我们可以写0.33。

表示循环数字的另一种方法是使用条在循环数字上方，就像我们下面展示的一样。

= 0.3333…… = 0.3

因此，分数 的小数是 0.3。