如何计算标准差

标准差是研究变异（离散程度）的最重要和广泛使用的度量。它显示了数据的变异性。标准差的计算有点复杂。犯错的风险很高，因此我们需要高度注意和精确计算。在本节中，我们将学习如何找到标准差。

标准差定义

标准差（SD）是一种量化指标，用于衡量数据集相对于其均值的分布（离散程度）。它被计算为方差的平方根。它由希腊小写字母σ（西格玛）表示。偏差越大，离散程度越大；偏差越小，均匀性越大。

其他一些定义是

• 标准差是衡量所有值相对于均值的变异程度。
• 标准差是各偏差平方和除以观测值数量的平方根。
• 它是方差的平方根。

变化

它定义了一个随机变量与其期望值相差多少。它是期望值与单个值之间差异平方的平均值。它永远不会有负值。它用σ²表示。方差的公式是

如何计算标准差

它通过确定每个数据点相对于均值的变异性来计算为方差的平方根。标准差越高，每个数据集与均值之间的方差就越高。

标准差的公式

有两种计算标准差的公式。这两种公式都衡量变异性。但它们之间存在差异。

• 总体标准差
• 样本标准差

总体标准差

它是一个参数，从总体中的每个个体计算一个固定值。总体标准差的公式是

其中

σ：总体标准差。

x_i：数据集中的每个元素。其中i = 1, 2, 3, ...., N。

μ：数据集中所有元素的均值。

N：元素的数量。

样本标准差

它是一个统计量。在这种标准差中，只取总体中的一些个体进行计算。它具有更大的变异性，因为它取决于样本。因此，样本的标准差大于总体标准差。

样本标准差的公式是

其中

s：样本标准差。

x_i：数据集中的每个元素。其中i = 1, 2, 3, ...., N。

x：数据集中所有元素的均值。

N：元素的数量。

现在，我们将看看这些标准差是如何相互不同的。考虑样本和总体标准差公式；我们发现这两个公式几乎相同。

步骤1：首先，计算平均值。将所有值相加并除以元素的数量。

步骤2：计算与平均值的偏差。为此，从每个值中减去平均值。

步骤3：将偏差平方。

步骤4：将偏差平方并相加。

步骤5：将平方偏差除以观测值的数量。此步骤是总体标准差和样本标准差之间的主要区别。

• 使用总体标准差时，将平方偏差之和除以N（元素的数量或观测值）。
• 使用样本标准差时，将平方偏差之和除以N-1（比元素或观测值数量少1）。

步骤6：找到我们上一步得到的商的平方根。

总体和样本标准差的值取决于N。N的值越大，总体和样本标准差越大。

标准差的性质

• 标准差的值永远不会是负数。
• 低偏差表示数据点倾向于非常接近均值。
• 高偏差表示数据点分布在一个较大的值范围上。
• 如果我们将一个常数添加到所有数据集中，它不会影响标准差。
• 如果我们将一个常数乘以所有数据集，它会影响标准差。
• 当且仅当所有观测值具有相同值时，标准差才能为零。

标准差的用途

• 它广泛用于生物学研究、统计学和金融领域。
• 它用于将正态曲线拟合到频率分布。
• 它用于衡量离散度。
• 它还用于金融领域，以计算金融风险。

标准差的方法

直接法

我们也可以使用直接法找到标准差。当偏差从实际均值中取出时使用它。直接法的公式是

其中

d=(x_i-x)

σ：标准差

x_i：数据集中的每个元素。其中i = 1, 2, 3, ...., N。

x：数据集中所有元素的均值。

N：元素的数量。

假设平均值法

在这种方法中，我们不计算实际平均值。相反，我们选择一个随机值来计算偏差。假定值必须位于中间值附近。它也称为快捷方法。假定平均值法的公式是

其中，

f：对应频率

d=x-A（A是假设平均值）

N：数据集中元素的数量。

步长偏差法

它是快捷方法的扩展形式。它简化了计算。假定平均值法的公式是

其中，

f：对应频率

d=（A是假设平均值）

N：数据集中元素的数量。

i：共同类间距

分布类型

在进入示例之前，我们必须了解三种类型的分布。

• 个体序列：个体序列是单列观测。例如

• 离散序列：在离散序列中，有两列。第一列包含观测值，第二列包含频率。例如

• 频率分布：频率分布也有两列。第一列包含观测值，第二列包含频率。观测值进一步分类为称为类的区间。例如

标准差公式
分发	直接法	假设平均值或快捷方法	步长偏差法
个体序列			-
离散序列			-
频率分布	-	-

个体序列示例

示例：使用直接法和假设平均值法找到以下数据的标准差。

解决方案

使用直接法

首先，我们将计算平均值。

现在，我们将计算方差 (σ²)。

方差的公式是：

将值代入方差公式，我们得到

标准差的公式是： σ =√σ²

σ =√310.625=17.624
σ =17.624

使用假设平均值或快捷方法

我们知道个体序列的假设平均值法公式

在上述公式中，d=x-A。其中A是假设平均值。所以，我们假设A = 38。

将值代入上述公式，我们得到

离散序列示例

示例：使用直接法和快捷方法找到以下数据的标准差。

解决方案

使用直接法

首先，我们将计算平均值。

我们知道离散序列的直接法公式

将值代入公式，我们得到

使用快捷方法

我们知道离散序列的快捷方法公式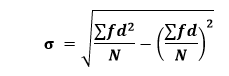

在上述公式中，d=x-A。其中A是假设平均值。所以，我们假设A = 6.5。

将值代入公式，我们得到

因此，标准差为1.148。

频率分布示例（分组数据或连续序列）

示例：使用直接法和快捷方法计算以下数据的标准差。

解决方案

使用步长偏差法

我们知道连续序列的步长偏差法公式

在上述公式中，。其中A是假设平均值。所以，首先，我们将计算每个类区间的平均值（m）。在下表中，我们计算了每个类区间的平均值。其中，我们假设平均值为35。

分数 (x)	f			d2	fd	fd2
0-10	15	5	-3	9	-45	135
10-20	15	15	-2	4	-30	60
20-30	23	25	-1	1	-23	23
30-40	22	35 (A)	0	0	0	0
40-50	25	45	1	1	25	25
50-60	10	55	2	4	20	40
60-70	5	65	3	9	15	45
70-80	10	75	4	16	40	160
	∑f=N=125				∑fd=2	∑fd2=488

将值代入公式，我们得到

总体标准差示例

示例：使用总体标准差找到标准差。

12, 2, 45, 23, 55, 8, 11, 19, 57, 3

解决方案

在上述问题中，给出了十名学生的成绩。问题要求应用样本标准差。在这种情况下，我们不会将所有学生的成绩都用于计算。我们将取少量学生的成绩作为样本进行计算。

我们只取了六个成绩进行计算，如下所示

12, 45, 23, 11, 19, 3

我们知道样本标准差的公式

现在，我们将找到公式中使用的值。

步骤1：计算样本平均值 (x)。

步骤2：对于每个数据元素，减去平均值并平方结果。

步骤3：将 ∑(x_i-x)² 除以 N-1。这里共有6个元素，所以将总和除以6-1=5，我们得到

步骤4：取上述结果的平方根。

s =√209.2=14.46

因此，样本标准差为14.46。

样本标准差示例

示例：使用总体标准差找到标准差。

12, 2, 45, 23, 55, 8, 11, 19, 57, 3

解决方案

在上述问题中，给出了十名学生的成绩。问题要求应用总体标准差。在这种情况下，我们将取所有学生的成绩进行计算。

我们知道样本标准差的公式

现在，我们将找到公式中使用的值。

步骤1：计算总体平均值 (μ)。

步骤2：对于每个数据元素，减去平均值并平方结果。

步骤3：将 ∑(x_i-μ)² 除以 N。这里共有10个元素，所以将总和除以10，我们得到

步骤4：取上述结果的平方根。

σ =√401=20.02=20

因此，总体标准差为20。