如何计算三角形的面积和周长

你是否见过吉萨大金字塔、悉尼歌剧院或埃菲尔铁塔？你知道它们有什么共同点吗？尽管风格迥异，但这些建筑奇迹都采用了我们都熟知的几何形状——三角形。三角形引人入胜且用途广泛，涵盖数学、科学、工程、艺术和设计等众多领域。在本文中，我们将学习三角形是什么，以及如何计算它们的面积和周长。

什么是三角形

三角形是一个简单的二维形状，有三条直线边和三个角。它看起来像一个“V”形的平面图形。三角形的三个角之和为 180 度，三条边的总长度决定了三角形的大小和形状。三角形是几何学中的基本形状，在许多日常物品中都可以找到，从屋顶到标识，甚至三明治。

三角形的分类

三角形通常根据边的长度或角的度数进行分类。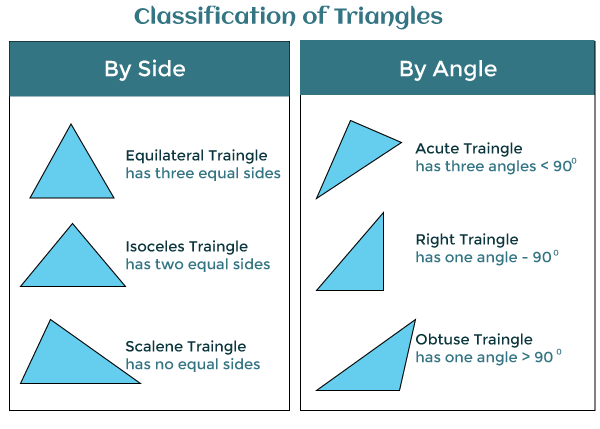

• 按边长分类的三角形
  
  1. 等边三角形：三边长度都相等的三角形，三个角都为 60 度。
  2. 等腰三角形：有两条边长度相等，两个角度数也相等的三角形。
  3. 不等边三角形：三条边长度都不相等，三个角度数也都不相等的三角形。
• 按角度分类的三角形
  
  1. 锐角三角形：每个角都小于 90 度的三角形称为锐角三角形。
  2. 钝角三角形：有一个角大于 90 度的三角形称为钝角三角形。
  3. 直角三角形：有一个角恰好为 90 度的三角形称为直角三角形。

这些分类并非互斥。一个三角形可以同时属于一个或多个类别。例如，等边三角形也是锐角三角形，因为它的三个角都小于 90 度。同样，如果直角三角形的两条直角边长度相等，它也可以是等腰三角形。

三角形的周长

三角形的周长是其三条边长度的总和。它是通过将边的长度相加来计算的。如果一个三角形的边长分别为 a、b 和 c，则周长 P 由公式给出

示例：求一个边长分别为 5 厘米、7 厘米和 9 厘米的三角形的周长。

解决方案

三角形的周长 = 三角形所有边长之和

= 5 厘米 + 7 厘米 + 9 厘米

= 21 厘米

三角形面积

三角形的面积是指由其三条边围成的区域。它被定义为三角形边界内的空间大小。三角形的面积可以通过各种方法计算，具体取决于已知的三角形尺寸和角度。

已知高的情况下计算三角形的面积

计算三角形面积最简单的方法是已知其底和高。计算已知底和高的三角形面积的公式是

示例：求一个底为 8 厘米、高为 5 厘米的三角形的面积。

解决方案

三角形面积 = ½ * 底 * 高

= ½ * 8 厘米 * 5 厘米

= 4 * 5

= 20 平方厘米

等边三角形的面积（未知高）

我们可以在不知道高的情况下，通过边长来计算等边三角形的面积。边长为 a 的等边三角形的面积公式是

示例：求一个边长为 6 厘米的等边三角形的面积。

解决方案

等边三角形面积 = √3/4 * a^2

= √3/4 * 6^2

= √3/4 * 36

= 9√3 平方厘米

仅已知边长的等腰三角形的面积

我们可以在不知道高的情况下，通过边长来计算等腰三角形的面积。等边为 a、底边为 b 的等腰三角形的面积公式是

这个公式是通过将等腰三角形分成两个直角三角形，并使用勾股定理来计算其高度推导出来的。

示例：求一个等边为 5 厘米、底边为 6 厘米的等腰三角形的面积。

解决方案

面积 = ¼ * b * √(4a^2 - b^2)

= ¼ * 6 * √(4 * 5^2 - 6^2)

= ¼ * 6 * √(100 - 36)

= ¼ * 6 * √64

= ¼ * 6 * 8

= 6 * 2

= 12 平方厘米

海伦公式：计算仅已知边长的面积

海伦公式，以古希腊数学家亚历山大·希罗的名字命名，用于计算已知三边长度的三角形的面积。当我们知道三角形的边长但不知道其高时使用海伦公式。计算边长为 a、b、c 的三角形面积的海伦公式是

这里，s 是三角形的半周长，计算方法是：

示例：求一个边长分别为 9 厘米、12 厘米和 15 厘米的三角形的面积。

解决方案

半周长 (s) = (a + b + c)/2

= (9 厘米 + 12 厘米 + 15 厘米)/2

= 36/2 厘米

= 18 厘米

面积 = √(s * (s - a) * (s - b) * (s - c))

= √(18 * (18 - 9) * (18 - 12) * (18 - 15))

= √(18 * 9 * 6 * 3)

= √2196

= 54 平方

结论

三角形是一个简单的二维形状，有三条直线边和三个角。三角形的三个角之和总是 180 度，三角形的大小和形状由其三条边的总长度决定。三角形是几何学中的基本形状，可以在各种日常物品中看到。它们的通用性和应用性使它们成为数学、科学、工程和设计等许多学科的重要组成部分。